Systolic inequality on the 2-torus

Conan5 Comments

Starting last summer with professor Guth, I’ve been interested in the systolic inequality for Riemannian manifolds. As a starting point of a sequence of short posts I plan to write on little observations I had related to the subject, here I’ll talk about the baby case where we find the lower bound of the systole on the 2-torus in terms of the area of the torus.

Given a Riemannian manifold (M, g) where g is the Riemannian metric.

Definition: The systole of M is the length of smallest homotopically nontrivial loop in M.

We are interested in bounding the systole in terms of the n-th root of the volume of the manifold ( where n is the dimension of M ).

Note that the systole is only defined when our manifold has non-trivial fundamental group. I wish to remark that for the case of n-torus, having an inequality of the form (\mbox{Sys}(\mathbb{T}^n))^n \leq C \cdot \mbox{Vol}(\mathbb{T}^n) is intuitive as we can see in the case of an embedded 2-torus in \mathbb{R}^3, we may deform the metric (hence the embedding) to make a non-contactable loop as small as we want while keep the volume constant, however when we attempt to make the smallest such loop large when not changing the volume, we can see that we will run into trouble. Hence it’s expected that there is an upper bound for the length of the smallest loop.

Since if only one loop in some homotopy class achieves that minimal length, we should be able to enlarge it and contract some other loops in that class to enlarge the systole and keep the volume constant. Hence it’s tempting to assume that all loops in the same class are of the same length. In the 2-torus case, such thing is the flat torus. Since any flat torus has systole proportional to (\mbox{Vol}(\mathbb{T}^2))^{\frac{1}{2}}, we have reasons to expect the optimal case fall inside this family. i.e.

(\mbox{Sys}(\mathbb{T}^2))^2 \leq C \cdot \mbox{Vol}(\mathbb{T}^2).

This is indeed the case. The result was given in an early unpublished result by Loewner.

Let’s first optimize in the class of flat torus:

My first guess was that C cannot be made less than 1 i.e. the torus \mathbb{R}^2/ \mathbb{Z}^2 is the optimum case. However, this is not true. Let’s be more careful:

\mathbb{T}^2 = \mathbb{R}^2 / (0,c)\mathbb{Z} \times (a, b)\mathbb{Z}

Since by scaling does not change ratio between (\mbox{Vol}(\mathbb{T}^2)) and (\mbox{Sys}(\mathbb{T}^2))^2, we may normalize and let c=1

Let \alpha, \beta be generators of the fundamental group of \mathbb{T}^2 length of all geodesic loops in class [\alpha], \ [\beta] are the side lengths of the parallelepiped i.e. 1 and ||(a,b)||. W.L.O.G we suppose a, b > 0. \alpha \beta^{-1} has length ||((1-a),b)|| and all geodesics in other classes are at least twice as long as one of the above three.

Hence the systole is maximized when those three are equal, we get a=1/2, b=\sqrt{3}/2. The systole in this case is 1 and the volume is \sqrt{3}/2. Hence for any flat torus, we have

(\mbox{Sys}(\mathbb{T}^2))^2 \leq \frac{2}{\sqrt{3}} \cdot \mbox{Vol}(\mathbb{T}^2).

Theorem (Loewner): This bound holds for any metric g on \mathbb{T}^2.

Proof: We will show this by reducing the case to flat metric.

g induced an almost complex structure on \mathbb{T}^2, on surfaces, any almost complex structure is integrable. Hence there exists f:\mathbb{T}^2 \rightarrow \mathbb{R}^+ and g= f \dot g_0 where (\mathbb{T}^2, g_0) is a Riemann surface.

By uniformization theorem, (\mathbb{T}^2, g_0) is the quotient of \mathbb{C} by a discrete lattice. i.e. (\mathbb{T}^2, g_0) is a flat torus \mathbb{R}^2 / (0,c)\mathbb{Z} \times (a, b)\mathbb{Z}.

By scaling of the torus, we may assume the volume of the manifold is 1 i.e.

\displaystyle \int_{\mathbb{T}^2} f \ dV_{g_0} = 1 = \mbox{Vol}(\mathbb{T}^2, g_0)

Any nontrivial homotopy class of loops on (\mathbb{T}^2, g) can be represented by a straight loop on the flat torus. The length of such a loop in (\mathbb{T}^2, g) is merely integration of f along the segment.

Here we have a family of loops in the homotopy class that is straight, by taking a segment of appropriate length orthogonal to the loops, we have the one-parameter family of parallel loops foliate the torus. Hence integrating over the segment of the length of the loops gives us the total volume of the torus. By Fubini, we have at least one loop is longer than volume of the torus over length of the segment we integrated on, which is the length of the straight loop in the flat torus.

Therefore the systole of (\mathbb{T}^2, g) is smaller than the minimum length of straight loops which is smaller than that of the flat torus. While the volume are the same. Hence it suffice to optimize the ratio in the class of flat tori. Establishes the theorem.

Combining the pervious statement, we get

(\mbox{Sys}(\mathbb{T}^2))^2 \leq \frac{2}{\sqrt{3}} \cdot \mbox{Vol}(\mathbb{T}^2)

for any metric on the torus.

5 thoughts on “Systolic inequality on the 2-torus”

  1. Hi Conan Wu,
    I read with interest your piece on Area 777. Note a similar article by Yongwhan Lim at Stanford. Are you interested in generalisations of Loewner’s inequality?
    MK

    Like

    Reply

    • Yes, indeed I’m interested in generalizations of Loewner’s inequality. IN particular, I read about Gromov’s proof for the higher dimension version for bounding systoles on the n-torus via filling radius. However the problem is open for general 3-manifolds and there can be generalizations on loops in multiple homotopy classes.

      I do not know Yongwhan Lim’s article, though…Any references?

      Like

      Reply

      • Opps, in fact by 3-manifolds I meant to say surfaces (other than the torus). i.e. bounding the sum of the lengths or the maximum length of loops in a pant decomposition of a high genus surface. Very sorry for the confusion. I guess we can also consider semilar questions for 3-mailfolds other than the torus (maybe pick families of loops in different homotopy classes? I do not know) Finding higher dimensional analogue of the ‘loop’ is hopeless via the Gromov-Katz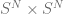 S^N \times S^N counterexamples for manifold with large dimension, but I do not know about non-contratible surfeces in 3-manifolds.

        By the way, nice article by Lim, Thank a lot~

        Like

Leave a comment