This is one of those items I should have written about long ago: I first heard about it over a lunch chat with professor Guth; then I was in not one, but two different talks on it, both by Peter Jones; and now, finally, after it appeared in this algorithms lecture by Sanjeev Arora I happen to be in, I decided to actually write the post. Anyways, it seem to live everywhere around my world, hence it’s probably a good idea for me to look more into it.
Has everyone experienced those annoy salesman who keeps knocking on you and your neighbors’ doors? One of their wonderful properties is that they won’t stop before they have reached every single household in the area. When you think about it, in fact this is not so straight foreword to do; i.e. one might need to travel a long way to make sure each house is reached.
Problem: Given points in
, what’s the shortest path that goes through each point?
Since this started as an computational complexity problem (although in fact I learned the analysts’s version first), I will mainly focus on the CS version.
Trivial observations:
In total there are about paths, hence the naive approach of computing all their lengths and find the minimum takes more than
time. (which is a long time)
This can be easily improved by a standard divide and concur:
Let be our set of points. For each subset
, for each
, let
length of shortest path from
to
going through all points in
.
Now the value of this can be computed recursively:
,
;
Otherwise
What we need is minimum of where
. There are
subsets of
, for any subset there are
choices for each of
.
is a minimum of
numbers, hence
time (as was mentioned in this pervious post for selection algorithm). Summing that up, the running time is
, slightly better than the most naive way.
Can we make it polynomial time? No. It’s well known that this problem is NP-hard, this is explained well in the wikipedia page for the problem.
Well, what can we do now? Thanks to Arora (2003), we can do an approximate version in polynomial time. I will try to point out a few interesting ideas from that paper. The process involved in this reminded me of the earlier post on nonlinear Dvoretzky problem (it’s a little embracing that I didn’t realize Sanjeev Arora was one of the co-authors of the Dvoretzky paper until I checked back on that post today! >.< ) it turns out they have this whole program about ‘softening’ classic problems and produce approximate versions.
Approximate version: Given points in
,
, find a path
through each point such that length
.
Of course we shall expect the running time to be a function of
and
, as
it shall blow up (to at least exponential in
, in fact as we shall see below, it will blow up to infinity).
The above is what I would hope is proved to be polynomial. In reality, what Arora did was one step more relaxed, namely a polynomial time randomized approximate algorithm. i.e. Given and
, the algorithm produces a path
such that
. In particular this means more than half the time the route is within
to the optimum.
Theorem (Arora ’03): for the randomized approximate algorithm.
Later in that paper he improved the bound to , which remains the best know bound to date.
Selected highlights of proof:
One of the great features in the approximating world is that, we don’t care if there are a million points that’s extremely close together — we can simply merge them to one point!

More precisely, since we are allowing a multiplicative error of , we also have trivial bound
, Hence the length can be increased by at least
which means if we move each point by a distance no more than
and produce a path
connecting the new points with
, then we can simply get our desired
from
, as shown:
i.e. the problem is “pixelated”: we may bound in a square box with side length
, divide each side into
equal pieces and assume all points are in the center of the gird cell it lies in (for convenience later in the proof we will assume
is a power of
, rescale the structure so that each cell has side length
. Now the side length of the box is
):
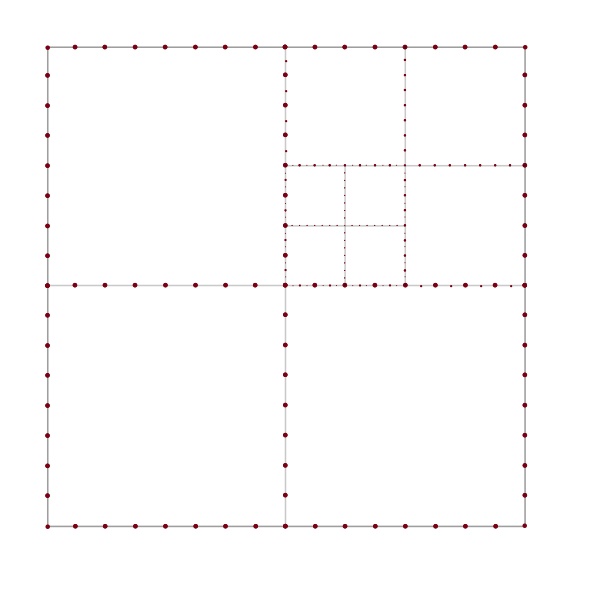
Now we do this so-called quadtree construction to separate the points (reminds me of Whitney’s original proof of his extension theorem, or the diatic squares proof of open sets being countable) i.e. bound in a square box and keep dividing squares into four smaller ones until no cell contains more than one point.
In our case, we need to randomize the quad tree: First we bound in a box that’s 4 times as large as our grid box (i.e. of side length
), shift the larger box by a random vector
and then apply the quad tree construction to the larger box:
At this point you may wonder (at least I did) why do we need to pass to a larger square and randomize? From what I can see, doing this is to get
Fact: Now when we pick a grid line at random, the probability of it being an th level dividing line is
.
Keep this in mind.
Note that each site point is now uniquely defined as an intersection of no more than nesting squares, hence the total number of squares (in all levels) in this quad tree cannot exceed
.
Moving on, the idea for the next step is to perturb any path to a path that cross the sides of the square at some specified finite set of possible “crossing points”. Let be the unique number such that
(will see this is the best
to choose). Divide sides of each square in our quad tree into
equal segments:
Note: When two squares of different sizes meet, since the number of equally squares points is a power of , the portals of the larger square are also portals of the smaller one.
With some simple topology (! finally something within my comfort zone :-P) we may assume the shortest portal-respecting path crosses each portal at most twice:
In each square, we run through all possible crossing portals and evaluate the shortest possible path that passes through all sites inside the square and enters and exists at the specified nodes. There are side length
possible entering-exiting configurations, each taking polynomial time in
(in fact
time) to figure out the minimum.
Once all subsquares has their all paths evaluated, we may move to the one-level larger square and spend another operations. In total we have
which is indeed polynomial in many operations.
The randomization comes in because the route produced by the above polynomial time algorithm is not always approximately the optimum path; it turns out that sometimes it can be a lot longer.
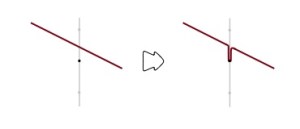
Expectation of the difference between our random portal respecting minimum path and the actual minimum
is bounded simply by the fact that minimum path cannot cross the grid lines more that
times. At each crossing, the edge it crosses is at level
with probability
. to perturb a level
intersection to a portal respecting one requires adding an extra length of no more than
:
P.S. You may find images for this post being a little different from pervious ones, that’s because I recently got myself a new iPad and all images above are done using iDraw, still getting used to it, so far it’s quite pleasant!
Bonus: I also started to paint on iPad~
–Firestone library, Princeton. (Beautiful spring weather to sit outside and paint from life!)