So~ After 2.5 weeks of wonderful math discussions with Amie and Charles, I finished my winter vacation and got back to Princeton! (and back to my normal blogging Sundays ^^)
One thing I would like to shear here is that we (me and Charles) finally got an answer to the following question that’s been haunting me for a while:
Question: Given Jordan curve containing a neighborhood of
in its interior. Given parametrizations
.
Is it true that for all , there exists
s.t. any Jordan curve
with a parametrization
so that
in the uniform norm implies the Riemann maps
from
to the interiors of
that fixes the origin and have positive real derivatives at
would be at most
apart?
i.e. Is the projection map from the space of parametrized Jordan curves (with the uniform metric) to the space of unparametrized Jordan curves (with metric given by taking uniform distance between the canonical Riemann maps) continuous?
First, I think the development and problem-solving process for this one is quite interesting and worth mentioning (skip this if you just want to see math):
—Begin story—
The problem was initially of interest because I stated a lemma on our Jordan curves paper which asserts the above projection map is continuous at smooth curves. To my surprise, I was unable to prove this seemingly-direct lemma. I turned to Charles for help, after a day or so of thinking he proved it for smooth curves (via a very clever usage of cross-cuts as in the proof of Carathedory’s theorem) and asked back whether the map is actually continuous at all points.
This seemed to be such a natural question but we couldn’t find it in the literature. For a day or so we were both feeling negative about this since the cross-cut method fails when the Jordan curve has positive measure, which “should” happen a lot. In any case, I posted a question on mathoverflow to see if there is a standard theorem out there implying this. Almost right after I posted the question, during a wonderful lunch-conversation with Charles, I got this wonderful idea of applying extremal length techniques not to the semi-circular crosscut but only to the ‘feet’ of it. Which later that day turned out to be a proof of the continuity.
The next morning, after confirming the steps of the proof and made sure it works, I was thrilled to find that Thurston responded to the post and explained his intuition that the answer is positive. Although having solved the problem already, I am still amazed by his insights ^^ (It’s the second question I asked there, he left an comment again! It just feels great to have your idol giving you ideas, isn’t it? :-P)
Later on, McMullen pointed out to us that in fact a book by Pommerenke contains the result. Nevertheless, it was great fun proving this, hence I decided to sketch the proof here ^^
—End story—
Ingredients of the proof: We quote the following well-known but weaker theorem (one can find this in, for example Goluzin’s classical book, p228)
Theorem: If the Jordan domains converge (in the sense that parametrizations of the boundaries converge uniformly) then the Riemann maps converge uniformly on compact sets.
We also use the following topological lemma:
Lemma: Given Jordan curve ,
be a parametrization. For all
, there exists
s.t. for all
with
( denote C' = \gamma'(S^1)$) , for all
,
where is the short arc in
connecting
.
The proof of the lemma is left as an exercise
Proof of the Theorem:
Given and
as in the theorem, apply the lemma to
, we obtain a
so that all curves
-close to
has the property that the arc connecting any two points less than
-apart has diameter no more than
.
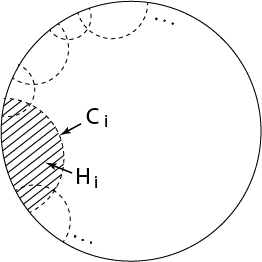
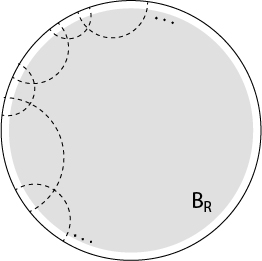
By compactness of , we can choose finitely many crosscut neignbourhoods
,
are "semi-discs" around points in
as shown:
By extremal length, we can choose the cross-cuts bounding
with length
where
is the canonical Riemann map corresponding to
. Hence by lemma, we also get
.
Let be endpoints of
.
Let .
Choose and
covers
. Let
:
By the above theorem in Goluzin, since is compact, there exists a
s.t.
.
Fix a with
. Let
be the canonical Riemann map corresponding to
.
Claim: .
First note that assuming the theorem in Goluzin, it suffice to show .
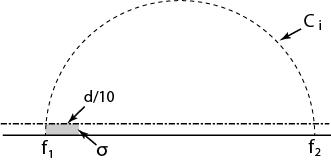
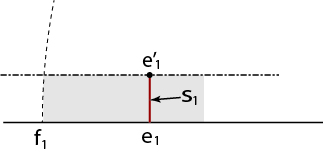
For any , let
be endpoints of
. Apply the extremal length to the set of radial segments in the almost-rectangle
.
We conclude there exists s.t. the segment
has length
.
Since and
, we have
.
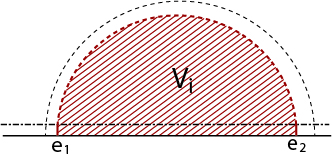
Similarly, find where
.
Connect by a semicircle contained in
, denote the enclosed region by
.
By construction, still covers
.
Hence for all , there exists
where
latex V_i$.
Since inside the two maps
are less than
apart, we have
.
Hence .
By construction, .
, we will break
into three parts and estimate diameter of each part separately.
Since ,
is another parametrization of
with
.
The arc connecting to
is contained in
, the arc in
connecting
is
away from
hence the union of the two has diameter at most
Length of the arcs are less than
.
Hence . By lemma, this implies the arc in
connecting
has length at most
.
Hence altogether the we have .
We deduce .
Q.E.D.