Tag: hyperbolic structure

A train track on twice punctured torus

Conan4 Comments

This is a non-technical post about how I started off trying to prove a lemma and ended up painting this:

One of my favorite books of all time is Thurston‘s ‘Geometry and Topology of 3-manifolds‘ (and I just can’t resist to add here, Thurston, who happen to be my academic grandfather, is in my taste simply the coolest mathematician on earth!) Anyways, for those of you who aren’t topologists, the book is online and I have also blogged about bits and parts of it in some old posts such as this one.

I still vividly remember the time I got my hands on that book for the first time (in fact I had the rare privilege of reading it from an original physical copy of this never-actually-published book, it was a copy on Amie‘s bookshelf, which she ‘robbed’ from Benson Farb, who got it from being a student of Thurston’s here at Princeton years ago). Anyways, the book was darn exciting and inspiring; not only in its wonderful rich mathematical content but also in its humorous, unserious attitude — the book is, in my opinion, not an general-audience expository book, but yet it reads as if one is playing around just to find out how things work, much like what kids do.

To give a taste of what I’m talking about, one of the tiny details which totally caught my heart is this page (I can’t help smiling each time when flipping through the book and seeing the page, and oh it still haunts me >.<):

This was from the chapter about Kleinian groups, when the term ‘train-track’ was first defined, he drew this image of a train(!) on moving on the train tracks, even have smoke steaming out of the engine:

To me such things are simply hilarious (in the most delightful way).

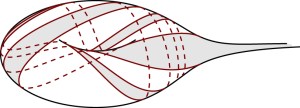
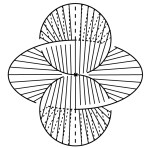
Many years passed and I actually got a bit more into this lamination and train track business. When Dave asked me to ‘draw your favorite maximal train track and test your tube lemma for non-uniquely ergodic laminations’ last week, I ended up drawing:

Here it is, a picture of my favorite maximal train track, on the twice punctured torus~! (Click for larger image)

Indeed, the train is coming with steam~

Since we are at it, let me say a few words about what train tracks are and what they are good for:

A train track (on a surface) is, just as one might expect, a bunch of branches (line segments) with ‘switches’, i.e. whenever multiple branches meet, they must all be tangent at the intersecting point, with at least one branch in each of the two directions. By slightly moving the switches along the track it’s easy to see that generic train track has only switches with one branch on one side and two branches on the other.

On a hyperbolic surface S_{g,p}, a train track is maximal if its completementry region is a disjoint union of triangles and once punctured monogons. i.e. if we try to add more branches to a maximal track, the new branch will be redundant in the sense that it’s merely a translate of some existing branch.

As briefly mentioned in this post, train tracks give natural coordinate system for laminations just like counting how many times a closed geodesic intersect a pair of pants decomposition. To be slightly more precise, any lamination can be pushed into some maximal train track (although not unique), once it’s in the track, any laminations that’s Hausdorff close to it can be pushed into the same track. Hence given a maximal train track, the set of all measured laminations carried by the train track form an open set in the lamination space, (with some work) we can see that as measured lamination they are uniquely determined by the transversal measure at each branch of the track. Hence giving a coordinate system on \mathcal{ML})(S).

Different maximal tracks are of course them pasted together along non-maximal tracks which parametrize a subspace of \mathcal{ML}(S) of lower dimension.

To know more about train tracks and laminations, I highly recommend going through the second part of Chapter 8 of Thurston’s book. I also mentioned them for giving coordinate system on the measured lamination space in the last post.

In any case I shall stop getting into the topology now, otherwise it may seem like the post is here to give exposition to the subject while it’s actually here to remind myself of never losing the Thurston type childlike wonder and imagination (which I found strikingly larking in contemporary practice of mathematics).

Filling and unfilling measured laminations

Conan2 Comments

(images are gradually being inserted ~)

I’m temporarily back into mathematics to (try) finish up some stuff about laminations. While I’m on this, I figured maybe sorting out some very basic (and cool) things in a little post here would be a good idea. Browsing through the blog I also realized that as a student of Dave’s I have been writing surprisingly few posts related to what we do. (Don’t worry, like all other posts in this blog, I’ll only put in stuff anyone can read and hopefully won’t be bored reading :-P)

Here we go. As mentioned in this previous post, my wonderful advisor has proved that the ending lamination space is connected and locally connected (see Gabai’08).

Definition: Let S_{g,p} be a hyperbolic surface of genus g and p punctures. A (geodesic) lamination L \subseteq S is a closed set that can be written as a disjoint union of geodesics. i.e. L = \sqcup_{\alpha \in I} \gamma_\alpha where each \gamma_\alpha is a (not necessary closed) geodesic, \gamma is called a leaf of L.

Let’s try to think of some examples:

i) One simple closed geodesic

ii) A set of disjoint simple closed geodesics

iii) A non-closed geodesic spirals onto two closed ones

iV) Closure of a single simple geodesic where transversal cross-sections are Cantor-sets

An ending lamination is a lamination where
a) the completement S \backslash L is a disjoint union of discs and once punctured discs (filling)
b) all leaves are dense in L. (minimal)

Exercise: example i) satisfies b) and example iv) as shown satisfies both a) and b) hence is the only ending lamination.

It’s often more natural to look at measured laminations, for example as we have seen in the older post, measured laminations are natural generalizations of multi-curves and the space \mathcal{ML}(S) is homeomorphic to \mathbb{R}^{6g-6+2p} (Thurston) with very natural coordinate charts (given by train-tracks).

Obviously not all measured laminations are supported on ending laminations (e.g. example i) and ii) with atomic measure on the closed curves.) It is well known that if a lamination fully supports an invariant measure, then as long as the base lamination satisfies a), it automatically satisfies b) and hence is an ending lamination. This essentially follows from the fact that having a fully supported invariant measure and being not minimal implies the lamination is not connected and hence won’t be filling.

Exercise:Example iii) does not fully support invariant measures.

Scaling of the same measure won’t effect the base lamination, hence we may eliminate a dimension by quotient that out and consider the space of projective measured laminations \mathcal{PML}(S) \approx \mathbb{S}^{6g-7+2p}. Hence we may decompose measured laminations into filling and unfilling ones. i.e.

\mathcal{PML}(S) = \mathcal{FPML}(S) \sqcup \mathcal{UPML}(S)

where \mathcal{FPML}(S) projects to the ending laminations via the forgetting measure map \pi.

This decomposition of the standard sphere \mathbb{S}^{6g-7+2p} is mysterious and very curious in my opinion. To get a sense of this, let’s take a look at the following facts:

Fact 1: \mathcal{UPML} is a union of countably many disjoint hyper-discs (i.e. discs of co-dimension 1).

Well, if a measured lamination is unfilling, it must contain some simple closed geodesic as a leaf (or miss some simple closed geodesic). For each such geodesic C, there are two possible cases:

Case 1: C is non-separating. The set of measured laminations that missed C is precisely the set of projective measured laminations supported on S_{g-1, p+2}, hence homeomorphic to \mathbb{S}^{6g-13+2p+4} = \mathbb{S}^{(6g-7+2p)-2} we may take any such measured lamination, disjoint union with C, we may assign any ratio of wrights to C and the lamination. This corresponds to taking the cone of \mathbb{S}^{(6g-7+2p)-2} with vertex being the atomic measure on C. Yields a disc of dimension (6g-7+2p)-1.

Case 2: C is separating. Similarly, the set of measured laminations missing C is supported on two connected surfaces with total genus g and total punctures p+2.

To describe the set of projective measured laminations missing C, we first determine the ratio of measure between two connected components and then compute the set of laminations supported in each component. i.e. it’s homeomorphic to [0,1] \times \mathbb{S}^{d_1} \times \mathbb{S}^{d_2}/\sim where d_1+d_2 = 6g-2*7+2(p+2) = 6g-10+2p and (0, x_1, y) \sim (0, x_2, y) and (1, x, y_1) \sim (1, x, y_2).

Exercise: check this is a sphere. hint: if d_1 =d_2 = 1, we have:

Again we cone w.r.t. the atomic measure corresponding to C, get a hyper disc.

At this point you may think ‘AH! \mathcal{UPML} is only a countable union of hyper-discs! How complicated can it be?!’ Turns out it could be, and (unfortunately?) is, quite messy:

Fact 2: \mathcal{UPML} is dense in \mathcal{PML}.

This is easy to see since any filling lamination is minimal, hence all leaves are dense, we may simply take a long segment of some leaf where the beginning and end point are close together on some transversal, close up the segment by adding a small arc on the transversal, we get a simple closed geodesic that’s arbitrarily close to the filling lamination in \mathcal{PML}. Hence the set of simple closed curves with atomic measure are dense, obviously implying \mathcal{UPML} dense.

So how exactly does this decomposition look like? I found it very mysterious indeed. One way to look at this decomposition is: we know two \mathcal{UPML} discs can intersect if and only if their corresponding curved are disjoint. Hence in some sense the configuration captures the structure of the curve complex. Since we know the curve complex is connected, we may start from any disc, take all discs which intersect it, then take all discs intersecting one of the discs already in the set, etc.

We shall also note that all discs intersecting a given disc must pass through the point corresponding to the curve at the center. Hence the result will be some kind of fractal-ish intersecting discs:

(image)

Yet somehow it manages to ‘fill’ the whole sphere!

Hopefully I have convinced you via the above that countably many discs in a sphere can be complicated, not only in pathological examples but they appear in ‘real’ life! Anyways, with Dave’s wonderful guidance I’ve been looking into proving some stuff about this (in particular, topology of \mathcal{FPML}). Hopefully the mysteries would become a little clearer over time~!

Gromov boundary of hyperbolic groups

Conan6 Comments

As we have seen in pervious posts, the Cayley graphs of groups equipped with the word metric is a very special class of geodesic metric space – they are graphs that have tons of symmetries. Because of that symmetry, we can’t construct groups with any kind of Gromov boundary we want. In fact, there are only few possibilities and they look funny. In this post I want to introduce a result of Misha Kapovich and Bruce Kleiner that says:

Let G be a hyperbolic group that’s not a semidirect product H \ltimes N where N is finite or virtually cyclic. (In those cases the boundary of G can be obtained from the boundary of H$).

Theorem: When G has 1-dimensional boundary, then the boundary is homeomorphic to either a Sierpinski carpet, a Menger curve or S^1.

OK. So what are those spaces? (don’t worry, I had no clue about what a ‘Menger curve’ is before reading this paper).

The Sierpinski carpet

(I believe most people have seen this one)

Start with the unit square, divide it into nine equal smaller squares, delete the middle one.

Repeat the process to the eight remaining squares.

and repeat…

Of course we then take the infinite intersection to get a space with no interior.

Proposition: The Sierpinski carpet is (covering) 1-dimensional, connected, locally connected, has no local cut point (meaning we cannot make any open subset of it disconnected by removing a point).

Theorem: Any compact metrizable planar space satisfying the above property is a Sierpinski carpet.

The Menger curve

Now we go to \mathbb{R}^3, the Menger curve is the intersection of the Sierpinski carpet times the unit interval, one in each of the x, y, z direction.

Equivalently, we may take the unit cube [0,1]^3, subtract the following seven smaller cubes in the middle:

In the next stage, we delete the middle ‘cross’ from each of the remaining 20 cubes:

Proceed, take intersection.

Proposition: The Menger curve is 1-dimensional, connected, locally connected, has no local cut point.

Note this is one dimensional because we can decompose the ‘curve’ to pieces of arbitrary small diameter by cutting along thin rectangular tubes, meaning if we take those pieces and slightly thicken them there is no triple intersections.

Theorem: Any compact metrizable nowhere planar (meaning no open set of it can be embedded in the plane) space satisfying the above property is a Menger curve.

Now we look at our theorem, infact the proof is merely a translation from the conditions on the group to topological properties of the boundary and then seeing the boundary as a topological space satisfies our universal properties.

A group being Gromov hyperbolic implies the boundary is compact metrizable.

No splitting over finite or virtually cyclic group implies the boundary is connected, locally connected and if it’s not S^1, then it has no local cut point.

Now what remains is to show, for groups, if the boundary is not planar then it’s nowhere planar. This is an easy argument using the fact that the group acts minimally on the boundary.

Please refer to first part of their paper for details and full proof of the theorem.

Remark: When study classical Polish-school topology, I never understood how on earth would one need all those universal properties (i.e. any xxx space is a xxx, usually comes with a long condition include ten or so items >.<). Now I see in fact such thing can be powerful. i.e. sometimes this allows us to actually get a grib on what does some completely unimaginable spaces actually look like!

Another wonderful example of this is the recent work of S. Hensel and P. Przytycki and the even more recent work of David Gabai which shows ending lamination spaces are Nobeling curves.

Proving the tameness conjecture

ConanLeave a comment

I have recently went through professor Gabai’s wonderful paper that gives a proof of the tameness conjecture. (This one is a simplified version of the argument given in Gabai and Calegari, where everything is done in the smooth category instead of PL). It’s been a quite exciting reading with many amazing ideas, hence I decided to write a summary from my childish viewpoint (as someone who knew nothing about the subject beforehand).

We say a manifold is tame if it an be embedded in a compact manifold s.t. the closure of the embedding is the whole compact manifold.

To motivate the concept, let’s look at surfaces: Any compact surface is, of course, tame. However, if we “shoot out” a few points of the surface to infinity, as the figure below, it become non-compact but still tame, as we can embed the infinite tube to a disk without a point.

Of course, we can also make a surface non-compact by shooting any closed subset to infinity (e.g. a Cantor set), but such construction will always result in a tame surface. (This can be realized using similar embeddings as above, we may embed the resulting surface into the original surface with image being the original surface subtract the closed set. If the closed set has interior, we further contract each interior components.)

On the other hand, any surface with infinite genus would be non-tame since if there is an embedding into a compact set, the image of ‘genesis’ would have limit points, which will force the compact space fail to be a manifold at that point.

Hence in spirit, being tame means that although the manifold may not be compact itself, but all topology happens in bounded regions (we can think of a complete embedding of the manifold into some \mathbb{R}^N so bounded make sense)

As usual, life gets more complicated for three-manifolds.

Tameness conjecture: Every complete hyperbolic 3-manifold with finitely generated fundamental group is tame.

A bubble chart for capturing the structure of the proof:

A few highlights of the proof: The key idea here is shrinkwrapping, very roughly speaking, to prove an geometrically infinite end is tame one needs to find a sequence of simplicial hyperbolic surfaces exiting at the end. Bonahon’s theorem gives us a sequence of closed geodesics exiting the end. By various pervious results, one is able to produce (topological) surfaces that are ‘in between’ those geodesics. Shrinkwrapping takes the given surface and shrinks it until it’s ‘tightly wrapped’ around the given sequence of geodesics. The fact that each of the curve the surface is wrapping around is a geodesic guarantees the resulting surface simplicial hyperbolic. (think of this as folding a piece of paper along a curve would effect its curvature, but alone a straight line would not; geodesics are like straight lines).

Once we have that, the remaining part would be showing the position of the surfaces are under control so that they would exit the end. Since simplicial hyperbolic surfaces has curvature \leq -1, by Gauss-Bonnet they have uniformly bounded area (given our surfaces also has bounded genus). By passing to a subsequence, we may choose the sequence of geodesics to be separated by some uniform constant, which will guarantee the wrapped surfaces are not too thin in the thick parts of the manifold, hence we have control over the diameter of the surface, from which we can conclude that the surfaces must exit the manifold.

Remark: Note that in general, unlike in two dimensions, a three manifold with finitely generated fundamental group does not need to be tame as the Whitehead manifold is homotopic to \mathbb{R}^3 (hence trivial fundamental group) but is not tame. On the other hand, if we have infinitely generated fundamental group, then the manifold can never be tame. The theorem says all examples of non-tame manifolds with finitely generated fundamental group does not admit hyperbolic structure.

A hyperbolic structure on the Whitehead link completement

Conan1 Comment

I’ve been going through Thurston’s book ‘The Geometry and Topology of Three-Manifolds‘ in a reading course with Amie Wilkinson. In Chapter 3, p32, when he’s constructing a hyperbolic structure on the Whitehead link complement, there is a picture on how to glue the 2-cells to the knot, to quite Thurston, ‘the attaching map for the two-cells are indicated by the dotted lines.’ However, for me it’s impossible to see where are the dotted lines going. So I reconstruct it here with some more clear pictures. The construction itself was a cool reading that I wish to share.

First, we have the Whitehead link, looking like the first figure below:

We attach three 1-cells (line segments) as in the second figure, note that the ‘x’ in the middle represents a line segment orthogonal to the screen, connecting the top and bottom line in the figure ‘8’ loop.

Now we will start to attach four 2-cells to the 1-complex above: First, we attach a 2-cell spanning the top part of the figure ‘8’ loop, spanning one side of the middle segment and two sides of the top segment (denote this by cell A):

Do the same with the bottom half (cell B). Note that each cell is attached to three edges, hence they are triangles without vertices in the knot complement with three one-cells attached.

For the other two cells, we attach as follows (cells C and D):

Combining the four 2-cells, we get something like the figure showed below. Note that at the top, cell A is under cell C in the left, intersecting the surface spanned by cells C and D at the edge, and comes above cell D to the right of the edge.

It’s easy to see that the complement of the above 2-complex does not separate \mathbb{R}^3, hence it’s a 3-cell with eight faces (i.e. it has to go through both sides of each 2-cell in order to fill the 3-space) each of its face has three edges. Hence we may glue an octahedron to the 2-complex after the gluing, pairs of faces of the octahedron will be identified groups of four edges will be identified to single edges. Hence to put a hyperbolic structure on the link complement, it suffice to put an hyperbolic structure to the octahedron with vertices deleted.

Since each edge is glued up by four edges of the octahedron, it suffice to find an octahedron (without vertices) in the hyperbolic 3-space that has all adjacent faces intersect in dihedral angle 2 \pi / 4 i.e. all adjecent faces are orthogonal in the hyperbolic space. But this is achieved if we inscribe the regular octahedron into the Klein model (also called projective model of hyperbolic 3-space.

The gluing map for the faces are merely rotations and reflections of the ball which are certainly hyperbolic isometries. Hence this gives a hyperbolic structure to the link complement.