Now we begin to prove the theorem.
4.Attractor-repeller pairs
Definition: A compact set 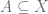 is an attractor for
is an attractor for 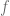 if there exists
if there exists 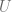 open,
open,  and
and 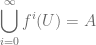 .
. 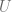 is called a basin of attraction.
is called a basin of attraction.
For any attractor 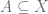 ,
, 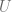 be a basin for
be a basin for  , let
, let  is open. By definition,
is open. By definition, 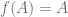 and
and  . We also have
. We also have
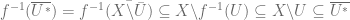
Definition: A repeller for 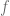 is an attractor for
is an attractor for  . A basin of repelling for
. A basin of repelling for 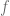 is a basin of attracting for
is a basin of attracting for  .
.
Hence  is a repeller for
is a repeller for 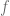 with basin
with basin 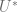 .
.
It’s easy to see that  is defined independent of the choice of basin for
is defined independent of the choice of basin for  . (Exercise)
. (Exercise)
We call such a pair 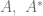 an attracting-repelling pair.
an attracting-repelling pair.
The following two properties of attracting-repelling pairs are going to be important for our proof of the theorem.
Proposition 1: There are at most countably many different attractors for 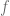 .
.
Proof: Since 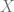 is compact metric, there exists countable basis
is compact metric, there exists countable basis 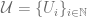 that generates the topology.
that generates the topology.
For any attractor  , any attracting basin
, any attracting basin  of
of  is a union of sets in
is a union of sets in  , i.e.
, i.e.  latex for some subsequence
latex for some subsequence  of
of 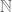 .
.
Since  is compact,
is compact, 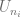 is an open cover of
is an open cover of  , we have some
, we have some  s.t.
s.t.  covers
covers  .
.
Let 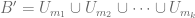 hence
hence  . We have
. We have
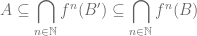
Since 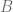 is an attracting basin for
is an attracting basin for  , all three sets are equal. Hence
, all three sets are equal. Hence 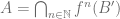 . i.e. any attractor is intersection of foreward interates of come finite union of sets in
. i.e. any attractor is intersection of foreward interates of come finite union of sets in  . Since
. Since  is countable, the set of all finite subset of it is coubtable.
is countable, the set of all finite subset of it is coubtable.
Hence there are at most countably many different attractors. This establishes the proposition.
By proposition 1, we let  be a list of all attractors for
be a list of all attractors for 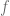 . Now we are going to relate the arrtactor-repeller pairs to the chain recurrent set and chain transitive components.
. Now we are going to relate the arrtactor-repeller pairs to the chain recurrent set and chain transitive components.
Proposition 2:

Proof: i) 
This is same as saying for any attractor  ,
,  .
.
For all  , let
, let 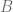 be a basin of
be a basin of  , then there is
, then there is  for which
for which  (recall that
(recall that  is the dual basin of
is the dual basin of 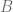 for
for  ). Since
). Since  and
and  we conclude
we conclude

Hence  . Let
. Let 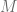 be the smallest integer for which
be the smallest integer for which  . Hence
. Hence  . Let
. Let 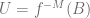 is also a basin for
is also a basin for  .
.
Now we show such  cannot be chain recurrent: Since
cannot be chain recurrent: Since  and
and  are compact and disjoint, we may let
are compact and disjoint, we may let
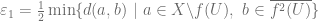
Since  , there exists some
, there exists some  s.t.
s.t.

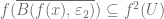 so there exists
so there exists  s.t.
s.t.
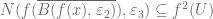
(Here  denotes the ball of radius
denotes the ball of radius  around
around 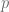 and
and 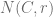 denotes the
denotes the  -neignbourhood of compact set
-neignbourhood of compact set 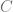 )
)
Now set 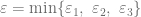 , for any
, for any  -chain
-chain  , we have: Since
, we have: Since 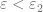 and
and  ,
,  and
and 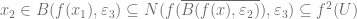 . Hence the third term of any such chain must be in
. Hence the third term of any such chain must be in 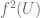 . Since
. Since  , no
, no  -chain starting at
-chain starting at 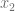 can reach
can reach  , in particular, the chain
, in particular, the chain  does not come back to
does not come back to  . Hence we conclude that
. Hence we conclude that  is not chain recurrent. ii)
is not chain recurrent. ii)  Suppose not, there is
Suppose not, there is 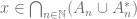 and
and  . i.e. for some
. i.e. for some  there is no
there is no  -chain from
-chain from  to itself. Let
to itself. Let 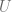 be the open set consisting all points that can be connected from
be the open set consisting all points that can be connected from  by an
by an  -chain.
-chain.
We wish to generate an attractor by 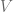 , to do this all we need to check is
, to do this all we need to check is  :
:
For any  there exists
there exists  with
with  . Since
. Since  , there is
, there is  -chain
-chain  which gives rise to
which gives rise to  -chain
-chain 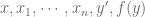 . Therefore
. Therefore  .
.
Hence  is an attractor with
is an attractor with 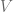 as a basin.
as a basin.
By assumption,  , since
, since  and there is no
and there is no  -chain from
-chain from  to itself,
to itself,  cannot be in
cannot be in  . i.e.
. i.e. 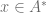 Take any limit point
Take any limit point  of
of  , since
, since  is compact
is compact 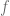 -invariant we have
-invariant we have  . But since we can find
. But since we can find  where
where  ,
,  gives an
gives an  -chain from
-chain from  to
to  , hence
, hence  .
.
Recall that 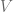 is a basin of
is a basin of  hence
hence 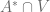 is empty. Contradiction. Establishes proposition 2.
is empty. Contradiction. Establishes proposition 2.
This proposition says that to study the chain recurrent set is the same as studying each attractor-repeller pair of the system. But the dynamics is very simple for each such pair as all points not in the pair will move towards the attractor under foreward iterate. We can see that such property is goint to be of importantce for our purpose since the dynamical for each attractor-repeller pair is like the sourse-sink map.
5. Main ingredient
Here we are going to prove a lemma that’s going to produce for us the ‘building blocks’ of our final construction. Namely a function for each attracting-repelling pair that strickly decreases along the orbits not in the pair. In light of proposition 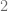 , we should expect to put those functions together to get our complete Lyapunov function.
, we should expect to put those functions together to get our complete Lyapunov function.
Lemma1: For each attractor-repeller pair  there exists continuous function
there exists continuous function ![g: X \rightarrow [0,1]](https://s0.wp.com/latex.php?latex=g%3A+X+%5Crightarrow+%5B0%2C1%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) s.t.
s.t. 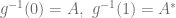 and
and  for all
for all  .
.
Proof: First we define ![\varphi: X \rightarrow [0,1]](https://s0.wp.com/latex.php?latex=%5Cvarphi%3A+X+%5Crightarrow+%5B0%2C1%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) s.t.
s.t.

Note that 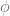 takes value
takes value 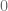 only on
only on  and
and 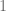 only on
only on  . However,
. However, 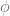 can’t care less about orbits of
can’t care less about orbits of 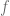 .
.
Define  . Hence automatically for all
. Hence automatically for all  ,
, 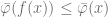 . Since no points accumulates to
. Since no points accumulates to  under positive iterations, we still have the
under positive iterations, we still have the  and
and  .
.
We now show that 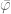 is continuous:
is continuous:
For 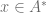 and
and  ,
,  and
and  hence
hence 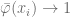 i.e.
i.e. 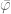 is continuous on
is continuous on  .
.
For  we use the fact that
we use the fact that  is attracting. Let
is attracting. Let 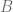 be a basin of
be a basin of  . For all
. For all 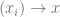 , for any
, for any  , there is
, there is  s.t.
s.t.  . Therefore for some
. Therefore for some  , all
, all  are in
are in  i.e.
i.e.  hence
hence 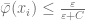 . But for some
. But for some 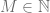 and all
and all  ,
,  . Therefore
. Therefore  .
. 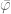 is continuous on
is continuous on  .
.
Let  , for any
, for any 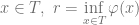 , since
, since  , there exists
, there exists 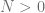 s.t. for all
s.t. for all 
![\varphi(f^n(T))\subseteq [0,r/2]](https://s0.wp.com/latex.php?latex=%5Cvarphi%28f%5En%28T%29%29%5Csubseteq+%5B0%2Cr%2F2%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) . i.e.
. i.e. 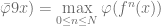 which is countinous. Since those ‘bands’
which is countinous. Since those ‘bands’ 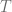 partitions the whole
partitions the whole 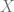 (by taking
(by taking 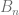 to be
to be 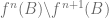 ), hence we have proven
), hence we have proven 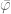 is continuous on the whole
is continuous on the whole 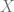 .
.
Finally, we define

We check that 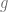 is continuous since
is continuous since 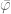 is.
is. 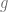 takes values
takes values 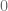 and
and 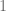 only on
only on  and
and  , respectively. For any
, respectively. For any  ,
,

therefore  iff
iff  for all
for all  i.e.
i.e. 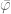 is constant on the orbit of
is constant on the orbit of  . But this cannot be since there is a subsequence of
. But this cannot be since there is a subsequence of 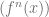 converging to some point in
converging to some point in  , continuity of
, continuity of 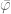 tells us this constant has to be
tells us this constant has to be 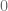 hence
hence  .
.
Therefore 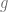 is strictly decreasing along orbits of
is strictly decreasing along orbits of 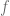 not in
not in  .
.
Establishes lemma 1.
6.Proof of the main theorem
The proof of the main theorem now follows easily from what we have established so far.
First we restate the fundamental theorem of dynamical systems:
Theorem: Complete Lyapunov function exists for any homeomorphisms on compact metric spaces.
Proof: First we enumerate the countably many attractors as  . For each
. For each 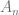 , we have function
, we have function 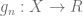 where
where 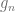 is
is 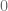 on
on 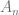 ,
, 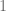 on
on  and is strictly decreasing on
and is strictly decreasing on  .
.
Define  by
by

Since each 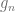 is bounded between
is bounded between 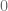 and
and 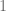 , the sequence of partial sums converge uniformly. Hence the limit function
, the sequence of partial sums converge uniformly. Hence the limit function 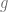 is continuous.
is continuous.
For points  , we have
, we have  for all
for all 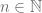 . i.e. $latex \ \forall n \in \N, \ g_n(p) = 0$ or
. i.e. $latex \ \forall n \in \N, \ g_n(p) = 0$ or  . Hence we have
. Hence we have
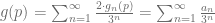
where each 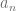 is in
is in  . This is same as saying the base-
. This is same as saying the base-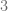 expansion of
expansion of 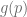 only contains digits
only contains digits 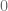 and
and 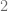 . We conclude
. We conclude  where
where 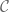 is the standard middle-third Cantor set in
is the standard middle-third Cantor set in ![[0, 1]](https://s0.wp.com/latex.php?latex=%5B0%2C+1%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) . i.e.
. i.e.  is compact and nowhere dense in
is compact and nowhere dense in 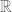 .
.
For 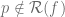 , there exists
, there exists 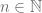 such that
such that  , hence
, hence 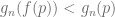 . This implies
. This implies  since
since  for all
for all  . i.e.
. i.e. 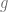 is strictly decreasing along orbits that are not chain recurrent.
is strictly decreasing along orbits that are not chain recurrent.
To show 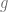 is constant only on the chain-transitive components, we need the following lemma:
is constant only on the chain-transitive components, we need the following lemma:
Claim:  are in the same chain-transitive component iff there is no attracting-repelling pair
are in the same chain-transitive component iff there is no attracting-repelling pair 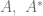 where one of
where one of  is in
is in  while the other in
while the other in  .
.
Proof (of claim): ” ” Suppose
” Suppose  and
and  , for any attractor
, for any attractor  , if
, if 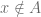 and
and 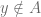 , then
, then 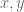 are both in
are both in  and we are done. Hence suppose at least one of
and we are done. Hence suppose at least one of 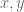 is in
is in  . W.L.O.G. suppose
. W.L.O.G. suppose  . Let
. Let 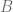 be a basin of
be a basin of  . Since
. Since 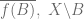 are closed and disjoint, we may choose
are closed and disjoint, we may choose  . By the same arguement as in proposition
. By the same arguement as in proposition 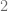 , there are no
, there are no 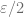 -chain (with length
-chain (with length  ) from any point in
) from any point in  to any point in
to any point in 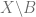 . Hence there is also no
. Hence there is also no 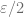 -chain from any point in
-chain from any point in  to any point in
to any point in  . Hence
. Hence  i.e.
i.e. 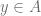 .
.
” ” Suppose for any attractor
” Suppose for any attractor  ,
,  iff
iff 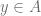 . For any
. For any  , let
, let 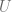 be the set of all points
be the set of all points  for which there is an
for which there is an  -chain from
-chain from  to
to  , as defined in proposition
, as defined in proposition 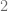 . We have showed in proposition
. We have showed in proposition 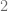 that
that 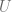 is a basin of some attractor
is a basin of some attractor  . Since
. Since  and
and  , hence
, hence  . Hence by our assumption,
. Hence by our assumption,  must be also in
must be also in  . Hence
. Hence  i.e. there is an
i.e. there is an  -chain from
-chain from  to
to  . Since the construction is symetric, we may also show there is an
. Since the construction is symetric, we may also show there is an  -chain from
-chain from  to
to  . i.e.
. i.e.  .
.
Establishes the claim.
Finally, for 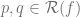 ,
, 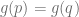 means
means 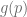 and
and 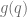 has the same base-
has the same base-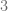 expansion in the Cantor set. This is same as saying
expansion in the Cantor set. This is same as saying 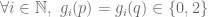 , which is to say there is no
, which is to say there is no  for which one of
for which one of  is in
is in  while the other in
while the other in  . Hence by Lemma, we conclude that
. Hence by Lemma, we conclude that 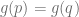 iff
iff  are in the same chain transitive component.
are in the same chain transitive component.
This establishes our theorem.
42.054805
-87.676354
, hence it’s a 3-cell with eight faces (i.e. it has to go through both sides of each 2-cell in order to fill the 3-space) each of its face has three edges. Hence we may glue an octahedron to the 2-complex after the gluing, pairs of faces of the octahedron will be identified groups of four edges will be identified to single edges. Hence to put a hyperbolic structure on the link complement, it suffice to put an hyperbolic structure to the octahedron with vertices deleted.
i.e. all adjecent faces are orthogonal in the hyperbolic space. But this is achieved if we inscribe the regular octahedron into the Klein model (also called projective model of hyperbolic 3-space.




