Month: September 2011

Kissing numbers of sphere packings

Conan1 Comment

Enough of the ‘trying to understand recent big theorems’ on this blog, let’s do something light and fun this week!

As I was browsing the ArXiv one day, one thing led to anther and I eventually arrived in a very short and cute paper of Greg Kuperberg and Oded Schramm.

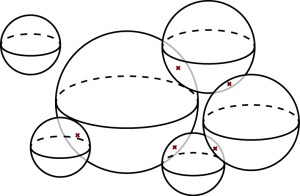
So, we have sphere packings, which is simply a bunch of spheres (say in \mathbb{R}^3) with disjoint interiors, some of them might be tangent to others, in which case we say the two sphere ‘kiss‘, like this: (points of tangency are marked with a red cross)

We can associate a graph to a sphere packing with vertices representing spheres and join two vertices with an edge if two sphere kisses:

Question: What kind of graph can appear this way?

Now if we go back to two-dimensions, it’s a classical theorem that any planar graph can appear as the nerve of a circle packing. (In fact, as mentioned at the end of this earlier post, something much stronger is true. i.e. it’s a theorem of Schramm that one can ‘kiss’ pretty much any given set of planar objects with a given nerve.)

In light of this, it’s nature to wonder whether every graph can be realized as a nerve of some sphere packing (since all graph embeds in some oriented surface which then embeds in \mathbb{R}^3). Turns out, no.

However I would imagine it’s not easy to show things such as a given graph cannot be realized. In the paper they came up with what’s perhaps the first restriction that shows not all graphs can be realized in such packing, namely:

The average kissing number is, as one might expect, in average how many kisses does each sphere get, i.e.

2 * number of tangency points / number of balls = 2|E|/|V|

If one thinks about it, how might one attempt to construct a packing with super large average kissing number? Well, perhaps we start with a single sphere, put a huge amount of small spheres around it (because one cannot fit many large spheres), then this middle one does get a lot of kisses, but what about the smaller ones? If they are equal sized then all the small spheres only gets roughly 7 kisses…now we need to put even smaller spheres around each of those…If we stop at any stage, there would be more smallers spheres that’s not taken care of than the larger ones with lots of kisses, so it’s not clear at all if the average can blow up.

As usual, things are much simpler in two dimensions: Since the Euler characteristic of any planar graph is 2 (|V|+|F|-|E|=2), and |F| \leq 2|E|/3 (any face needs at least 3 edges around them, precisely two faces share an edge) we have

|V| \geq |E|/3+2, hence 2|E|/|V| \leq 6 - 12/|V| < 6

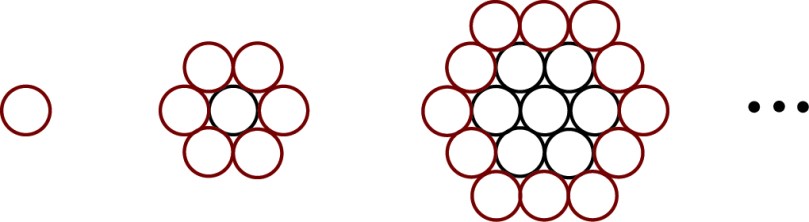
On the other hand, for our all-time favorite hexagonal packing of congruent circles, if we take more and more layers, the number of balls with six kisses grow like n^2, the number of balls on the boundary (hence with less than six kisses) is like n. Hence by adding enough layers we can make the average as close to 6 as we want~

Hexagonals are the best, as expected~

Now comes what’s in the paper: they showed that for any sphere packing, the average kissing number is less than 8+4\sqrt{3}. Hence any graph with average degree larger than 15 cannot be realized. They also provided an example of sphere packings with average kissing number larger than 12.

For simplicity I’ll only reproduce the ‘warm-up case’ in the paper which proves the kissing number is no more than 24. (well, since our goal here is only to say that not all graphs can be realized.) I find this observation (due to Schramm) is very simple, cute, and works in any dimensions.

Let’s first define some numbers:

k_c(n) = the maximum number of congruent sphere kissing one sphere (i.e. how many unit spheres we can place around a unit sphere) k_c can be easily computed, for example k_c(2) = 6 and k_c(3)=12, etc.

Let k(n) = \sup \{ average kissing number of sphere packings in dimension n \}. As we have seen k(2) = k_c(2) = 6 and we are interested in giving upper bounds to k(3).

Theorem: k(n) \leq 2 k_c(n).

Given a sphere packing P, let E be the set of kissing pairs and V be the set of spheres.

Define map f: E \rightarrow V where f maps each pair to the sphere in the pair with smaller radius (if the two spheres has the same radius, then just randomly choose one).

Since each sphere can only be surrounded by k_c(n) spheres of its size (of course larger than its size would give us fewer), we conclude that f is at most k_c to 1. Therefore, we have

|E| \leq k_c(n) |V|, i.e. k = 2|E|/|V| \leq 2k_c(n)

How simple!

Now going from 24 to 8+4\sqrt{3} requires some estimates relying on us being in 3-dimensions. Essentially, given any sphere in the packing, if we enlarge it by a ratio \lambda w.r.t its center, then this ‘shell’ intersect some other spheres in disjoint circles. Those circles of course cuts out a fraction of the area that’s < 1 on the shell. Summing this fraction over all \lambda shells results a number that’s less than |V|.

Now if we look at each pair of balls, say take pair (V_1, V_2), it turns out that if they kiss, the fraction of shell around V_1 that’s cut out by V_2 plus the fraction of shell around V_2 cut out by V_1 is a constant depending only on \lambda.

Hence we get a relation |V| \geq c(\lambda) \times |E|. Choose an optimum \lambda gives 8+4 \sqrt{3} which is a bit less than 15.

So we know k(3) \leq 8+4 \sqrt{3} but larger than 12, the problem of finding the exact value of k(3) remains open, so is the problem of giving other restrictions on the graph for being the nerve of a sphere packing.

Ultrametrics and the nonlinear Dvoretzky problem

Conan5 Comments

Hi guys~ The school year here at Princeton is finally (gradually) starting. So I’m back to this blog :-P

In this past week before anything has started, Assaf Naor came here and gave a couple rather interesting talks, which I decided to make a note about. For the complete content of the talk please refer to this paper by Naor and Mendel. As usual, I make no attempt on covering what was written on the paper nor what was presented in the talk, just some random pieces and bits which I found interesting.

A long time ago, Grothendieck conjectured what is now known as Dvoretzky’s theorem:

Theorem: For any D>1, for any k \in \mathbb{N}, there exists N depending only on k, D such that any normed vector space of dimension N or larger has a k-dimensional linear subspace that embeds (via a linear transformation) with distorsion at most D into the Hilbert space.

i.e. this says in the case where D is close to 1 (let’s write D = 1+\varepsilon) for any given k, *any* norm on a vector space of sufficiently high dimension will have a k dimensional subspace that looks almost Eculidean (meaning unit ball is round up to a multiple 1+\varepsilon).

Well, that’s pretty cool, but linear. As we all know, general metric spaces can be much worse than normed vector spaces. So here comes a nonlinear version of the above, posted by Terrence Tao:

Nonlinear Dvoretzky problem: Given \kappa>0, D>1, does there exist a \alpha so that every metric space of Hausdorff dimension \geq \alpha has a subset S of Hausdorff dimension \kappa that embeds into the Hilbert space with distorsion D?

Indeed, we should expect this to be a lot more general and much harder than the linear version, since we know literally nothing about the space except for having large Hausdorff dimension and as we know metric spaces can be pretty bizarre. That why we should find the this new result of theirs amazing:

Theorem 1 (Mendel-Naor): There is a constant C such that for any \lambda \in (0,1), every compact metric space with dimension \alpha has a closed subset S of dimension at least (1-\lambda) \alpha that admits an embedding into Hilbert space with distorsion C/ \lambda.

Note that, in the original linear problem, N = N(k, D) of course blows up to infinity whenever k \rightarrow \infty or D \rightarrow 1. (whenever we need a huge dimensional space with fixed ‘flatness’ or a fixed dimension but ‘super-flat’ subspace). That is, when we are looking for subspaces inside a random space with fixed (large) dimension N, the larger dimension we need, the less flat (more distorsion) we can expect it to be. i.e.

k \rightarrow N necessarily forces D \rightarrow \infty and
D \rightarrow 1 forces k \rightarrow 0.

We can see that this nonlinear theorem is great when we need large dimensional subspaces (when \lambda is close to 0), but not so great when we want small distorsion (it does not apply when distorsion is smaller than C, and blows up when it gets close to C).

In the original statement of the problem this gives not only that a large \alpha exists, but \alpha(\kappa, D) \leq \frac{D}{D-C} \kappa! In fact, when we are allowing relatively large distorsion (compare to constant C) this theorem is sharp:

Theorem 2 (Mendel-Naor): There exists constant C' and a family of metric spaces \{ X_\alpha \ | \ \alpha \in \mathbb{R}^+ \} such that for any small \varepsilon, no subset of X_\alpha with dimension \geq (1-\varepsilon)\alpha embeds into Hilbert space with distorsion \leq C'/\varepsilon.

This construction makes use of our all-time favorite: expander graphs! (see pervious post for definitions)

So what if D is small? Turns out, unlike in the linear case when D<2, there is no \alpha(\kappa, D), in the paper they also produced spaces X_\alpha for each \alpha where the only subset that embeds with distorsion < 2 are of Hausdorff dimension 0!

In his words, the proof of theorem 1 (i.e. the paper) takes five hours to explain, hence I will not do that. But among many neat things appeared in the proof, instead of embedding into the Hilbert space directly they embedded it into an ultrametric space with distorsion D, and then make use of the fact that any such space sits in the Hilbert space isometrically.

Definition: An ultrametric on space X is a metric with the additional property that for any three points x, y, z \in X, we have the so-called strong triangle inequality, i.e.

d(x, y) \leq \max \{ d(x, z), d(y,z) \}

If one pause and think a bit, this is a quite weird condition: for example, all triangles in an ultrametric space are isosceles with the two same length edge both longer than the third edge; every point is the center of the ball, etc.

Exercise: Come up with an example of an ultrametric that’s not the discrete metric, on an infinite space.

Not so easy, hum? My guess: the first one you came up with is the space of all words in 2-element alphabet \Sigma_2, with the dictionary metric (two points are distance 2^{-n} apart where n is the first digit they differ), right?

In fact in some sense all ultrametrics look like that. (i.e. they are represented by an infinite tree with weights assigned to vertices, in the above case a 2-regular tree with equal weights on same level) Topologically our \Sigma_2 is a Cantor set and sits isometrically in l_2. It’s not hard to see in fact all such space embeds isometrically in l_2.

I just want to say that this operation of first construct an ultrametric space according to our given metric space, embed, and then embed the ultrametric metric space into the Hilbert space somehow reminds me of when we want to construct a measure satisfying a certain property, we first construct it on a Cantor set, then divide up the space and use the values on parts of the Cantor set for parts of the space…On this vein the whole problem gets translated to producing a tree that gives the ultrametric and work with the tree (by no means simple, though).

Finally, let’s see a cute statement which can be proved by applying this result:

Urbanski’s conjecture: Any compact metric space of Hausdorff dimension > n can be mapped surjectively [thanks to Tushar Das for pointing out the typo] onto the unit ball B_1^n by a Lipschitz map.

(note strictly larger is important for our theorem to apply…since we need to subtract an \varepsilon) and hence another cute statement that’s still not known:

Question: Does any compact metric space with positive Hausdorff n-dimensional measure maps Lipschitzly onto B_1^n?