The Carnot-Carathéodory metric

March 22, 2011April 4, 2011 Conan7 Comments

I remember looking at Gromov’s notes “Carnot-Carathéodory spaces seen from within” a long time ago and didn’t get anywhere. Recently I encountered it again through professor Guth. This time, with his effort in explaining, I did get some ideas. This thing is indeed pretty cool~ So I decided to write an elementary introduction about it here. We will construct a such metric in $\mathbb{R}^3$ .

In general, if we have a Riemannian manifold, the Riemannian distance between two given points $p, q$ is defined as

$\inf_\Gamma(p,q) \int_0^1||\gamma'(t)||dt$

where $\Gamma$ is the collection of all differentiable curves $\gamma$ connecting the two points.

However, if we have a lower dimensional sub-bundle $E(M)$ of the tangent bundle (depending continuously on the base point). We may attempt to define the metric

$d(p,q) = \inf_{\Gamma'} \int_0^1||\gamma'(t)||dt$

where $\Gamma'$ is the collection of curves connecting $p, q$ with $\gamma'(t) \in E(M)$ for all $t$ . (i.e. we are only allowed to go along directions in the sub-bundle.

Now if we attempt to do this in $\mathbb{R}^3$ , the first thing we may try is let the sub-bundle be the say, $xy$ -plane at all points. It’s easy to realize that now we are ‘stuck’ in the same height: any two points with different $z$ coordinate will have no curve connecting them (hence the distance is infinite). The resulting metric space is real number many discrete copies of $\mathbb{R}^2$ . Of course that’s no longer homeomorphic to $\mathbb{R}^3$ .

Hence for the metric to be finite, we have to require accessibility of the sub-bundle: Any point is connected to any other point by a curve with derivatives in the $E(M)$ .

For the metric to be equivalent to our original Riemannian metric (meaning generate the same topology), we need $E(M)$ to be locally accessible: Any point less than $\delta$ away from the original point $p$ can be connected to $p$ by a curve of length $< \varepsilon$ going along $E(M)$ .

At the first glance the existence of a (non-trivial) such metric may not seem obvious. Let’s construct one on $\mathbb{R}^3$ that generates the same topology:

To start, we first identify our $\mathbb{R}^3$ with the $3 \times 3$ real entry Heisenberg group $H^3$ (all $3 \times 3$ upper triangular matrices with “1”s on the diagonal). i.e. we have homeomorphism

$h(x,y,z) \mapsto \left( \begin{array}{ccc} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{array} \right)$

Let $g$ be a left-invariant metric on $H_3$ .

In the Lie algebra $T_e(H_3)$ (tangent space of the identity element), the elements $X = \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) , Y = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array} \right)$ and $Z = \left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)$ form a basis.

At each point, we take the two dimensional sub-bundle $E(H_3)$ of the tangent bundle generated by infinitesimal left translations by $X, Y$ . Since the metric $g$ is left invariant, we are free to restrict the metric to $E(M)$ i.e. we have $||X_p|| = ||Y_p|| = 1$ for each $p \in M$ .

The interesting thing about $H_3$ is that all points are accessible from the origin via curves everywhere tangent to $E(H_3)$ . In other words, any points can be obtained by left translating any other point by multiples of elements $X$ and $Y$ .

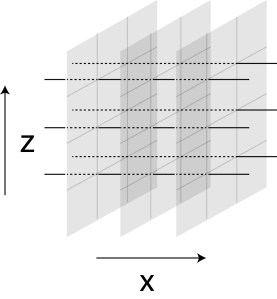
The “unit grid” in $\mathbb{R}^3$ under this sub-Riemannian metric looks something like:

Since we have

$\left( \begin{array}{ccc} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & x+1 & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{array} \right)$ ,

the original $x$ -direction stay the same, i.e. a bunch of horizontal lines connecting the original $yz$ planes orthogonally.

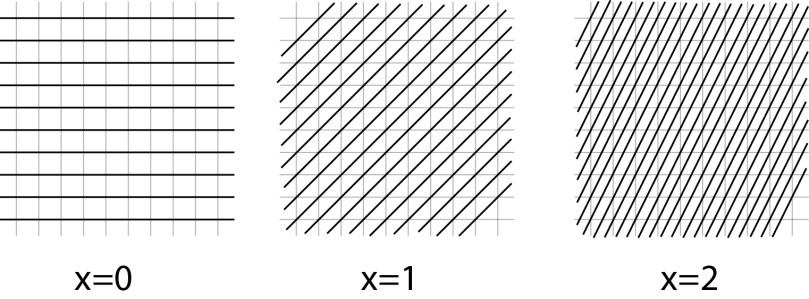
However, if we look at a translation by $Y$ , we have

$\left( \begin{array}{ccc} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & x & z+x \\ 0 & 1 & y+1 \\ 0 & 0 & 1 \end{array} \right)$

i.e. a unit length $Y$ -vector not only add a $1$ to the $y$ -direction but also adds a height $x$ to $z$ , hence the grid of unit $Y$ vectors in the above three $yz$ planes look like:

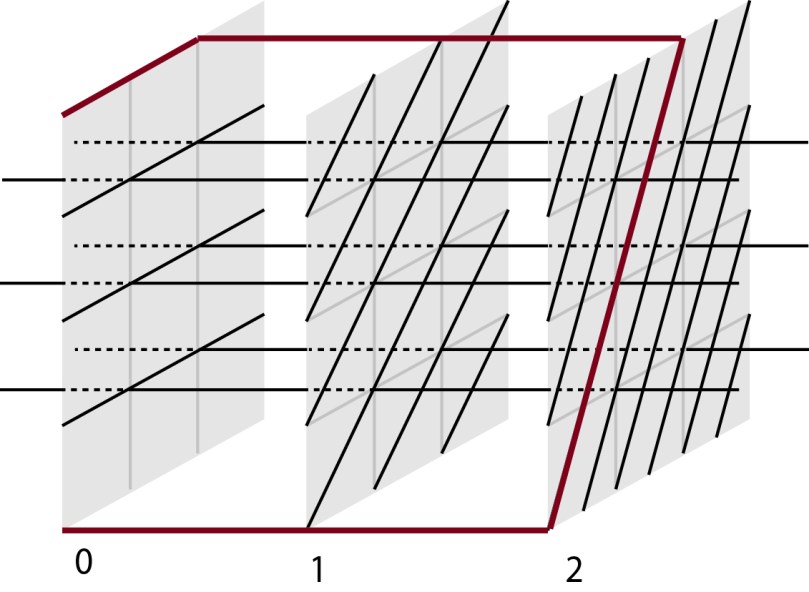
We can now try to see the rough shape of balls by only allowing ourselves to go along the unit grid formed by $X$ and $Y$ lines constructed above. This corresponds to accessing all matrices with integer entry by words in $X$ and $Y$ .

The first question to ask is perhaps how to go from $(0,0,0)$ to $(0,0,1)$ . –since going along the $z$ axis is disabled. Observe that going through the following loop works:

We conclude that $d_C((0,0,0), (0,0,1)) \leq 4$ in fact up to a constant going along such loop gives the actual distance.

At this point one might feel that going along $z$ axis in the C-C metric is always takes longer than the ordinary distance. Giving it a bit more thought, we will find this is NOT the case: Imagine what happens if we want to go from $(0,0,0)$ to $(0,0,10000)$ ?

One way to do this is to go along $X$ for 100 steps, then along $Y$ for 100 steps (at this point each step in $Y$ will raise $100$ in $z$ -coordinate, then $Y^{-100} X^{-100}$ . This gives $d_C((0,0,0), (0,0,10000)) \leq 400$ .

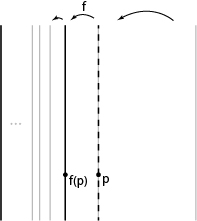
To illustrate, let’s first see the loop from $(0,0,0)$ to $(0,0,4)$ :

The loop has length $8$ . (A lot shorter compare to length $4$ for going $1$ unit in $z$ -direction)

i.e. for large $Z$ , it’s much more efficient to travel in the C-C metric. $d_C( (0,0,0), (0,0,N^2)) = 4N$

In fact, we can see the ball of radius $N$ is roughly an rectangle with dimension $R \times R \times R^2$ (meaning bounded from both inside and outside with a constant factor). Hence the volume of balls grow like $R^4$ .

Balls are very “flat” when they are small and very “long” when they are large.

A survey on ergodicity of Anosov diffeomorphisms

March 7, 2011November 1, 2011 Conan3 Comments

This is in part a preparation for my 25-minutes talk in a workshop here at Princeton next week. (Never given a short talk before…I’m super nervous about this >.<) In this little survey post I wish to list some background and historical results which might appear in the talk.

Let me post the (tentative) abstract first:

——————————————————

Title: Volume preserving extensions and ergodicity of Anosov diffeomorphisms

Abstract: Given a $C^1$ self-diffeomorphism of a compact subset in $\mathbb{R}^n$ , from Whitney’s extension theorem we know exactly when does it $C^1$ extend to $\mathbb{R}^n$ . How about volume preserving extensions?

It is a classical result that any volume preserving Anosov di ffeomorphism of regularity $C^{1+\varepsilon}$ is ergodic. The question is open for $C^1$ . In 1975 Rufus Bowen constructed an (non-volume-preserving) Anosov map on the 2-torus with an invariant positive measured Cantor set. Various attempts have been made to make the construction volume preserving.

By studying the above extension problem we conclude, in particular the Bowen-type mapping on positive measured Cantor sets can never be volume preservingly extended to the torus. This is joint work with Charles Pugh and Amie Wilkinson.

——————————————————

A diffeomorphism $f: M \rightarrow M$ is said to be Anosov if there is a splitting of the tangent space $TM = E^u \oplus E^s$ that’s invariant under $Df$ , vectors in $E^u$ are uniformly expanding and vectors in $E^s$ are uniformly contracting.

In his thesis, Anosov gave an argument that proves:

Theorem: (Anosov ’67) Any volume preserving Anosov diffeomorphism on compact manifolds with regularity $C^2$ or higher on is ergodic.

This result is later generalized to Anosov diffeo with regularity $C^{1+\varepsilon}$ . i.e. $C^1$ with an $\varepsilon$ -holder condition on the derivative.

It is a curious open question whether this is true for maps that’s strictly $C^1$ .

The methods for proving ergodicity for maps with higher regularity, which relies on the stable and unstable foliation being absolutely continuous, certainly does not carry through to the $C^1$ case:

In 1975, Rufus Bowen gave the first example of an Anosov map that’s only $C^1$ , with non-absolutely continuous stable and unstable foliations. In fact his example is a modification of the classical Smale’s horseshoe on the two-torus, non-volume-preserving but has an invariant Cantor set of positive Lebesgue measure.

A simple observation is that the Bowen map is in fact volume preserving on the Cantor set. Ever since then, it’s been of interest to extend Bowen’s example to the complement of the Cantor set in order to obtain an volume preserving Anosov diffeo that’s not ergodic.

In 1980, Robinson and Young extended the Bowen example to a $C^1$ Anosov diffeomorphism that preserves a measure that’s absolutely continuous with respect to the Lebesgue measure.

In a recent paper, Artur Avila showed:

Theorem: (Avila ’10) $C^\infty$ volume preserving diffeomorphisms are $C^1$ dense in $C^1$ volume preserving diffeomorphisms.

Together with other fact about Anosov diffeomorphisms, this implies the generic $C^1$ volume preserving diffeomorphism is ergodic. Making the question of whether such example exists even more curious.

In light of this problem, we study the much more elementary question:

Question: Given a compact set $K \subseteq \mathbb{R}^2$ and a self-map $f: K \rightarrow K$ , when can the map $f$ be extended to an area-preserving $C^1$ diffeomorphism $F: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ ?

Of course, a necessary condition for such extension to exist is that $f$ extends to a $C^1$ diffeomorphism $F$ (perhaps not volume preserving) and that $DF$ has determent $1$ on $K$ . Whitney’s extension theorem gives a necessary and sufficient criteria for this.

Hence the unknown part of our question is just:

Question: Given $K \subseteq \mathbb{R}^2$ , $F \in \mbox{Diff}^1(\mathbb{R}^2)$ s.t. $\det(DF_p) = 1$ for all $p \in K$ . When is there a $G \in \mbox{Diff}^1_\omega(\mathbb{R}^2)$ with $G|_K = F|_K$ ?

There are trivial restrictions on $K$ i.e. if $K$ separates $\mathbb{R}^2$ and $F$ switches complementary components with different volume, then $F|_K$ can never have volume preserving extension.

A positive result along the line would be the following slight modification of Moser’s theorem:

Theorem: Any $C^{r+1}$ diffeomorphism on $S^1$ can be extended to a $C^r$ area-preserving diffeomorphism on the unit disc $D$ .

For more details see this pervious post.

Applying methods of generating functions and Whitney’s extension theorem, as in this paper, in fact we can get rid of the loss of one derivative. i.e.

Theorem: (Bonatti, Crovisier, Wilkinson ’08) Any $C^1$ diffeo on the circle can be extended to a volume-preserving $C^1$ diffeo on the disc.

With the above theorem, shall we expect the condition of switching complementary components of same volume to be also sufficient?

No. As seen in the pervious post, restricting to the case that $F$ only permute complementary components with the same volume is not enough. In the example, $K$ does not separate the plane, $f: K \rightarrow K$ can be $C^1$ extended, the extension preserves volume on $K$ , and yet it’s impossible to find an extension preserving the volume on the complement of $K$ .

The problem here is that there are ‘almost enclosed regions’ with different volume that are being switched. One might hope this is true at least for Cantor sets (such as in the Bowen case), however this is still not the case.

Theorem: For any positively measured product Cantor set $C = C_1 \times C_2$ , the Horseshoe map $h: C \rightarrow C$ does not extend to a Holder continuous map preserving area on the torus.

Hence in particular we get that no volume preserving extension of the Bowen map can be possible. (not even Holder continuous)

Recurrence and genericity – a translation from French

January 31, 2011January 31, 2011 Conan1 Comment

To commemorate passing the French exam earlier this week (without knowing any French) and also to test this program ‘latex to wordpress‘, I decided to post my French-translation assignment here.

Last year, I went to Paris and heard a French talk by Crovisier. Strangely enough, although I can’t understand a single word he says, just by looking at the slides and pictures, I liked the talk. That’s why when being asked the question ‘so are there any French papers you wanted to look at?’, I immediately came up with this one which the talk was based on.

Here is a translation of selected parts (selected according to my interest) in section 1.2 taken from the paper `Récurrence et Généricité‘ ( Inventiones Mathematicae 158 (2004), 33-104 ) by C. Bonatti and S. Crovisier. In which they proved a connecting lemma for pseudo-orbits.

Interestingly, just in this short section they referred to two results I have discussed in earlier posts of this blog: Conley’s fundamental theorem of dynamical systems and the closing lemma. In any case, I think it’s a cool piece of work to look at! Enjoy~ (Unfortunately, if one wants to see the rest of the paper, one has to read French >.<)

Precise statements of results

1. Statement of the connecting lemma for pseudo-orbits

In all the following work we consider compact manifold ${M}$ equipped with an arbitrary Riemannian metric and sometimes also with a volume form ${\omega}$ (unrelated to the metric). We write ${\mbox{Diff}^1(M)}$ for the set of diffeomorphisms of class ${C^1}$ on ${M}$ with the ${C^1}$ topology and ${\mbox{Diff}^1_\omega(M) \subset \mbox{Diff}^1(M)}$ the subset preserving volume form ${\omega}$ .

Recall that, in any complete metric space, a set is said to be residual if it contains a countable intersection of open and dense sets. A property is said to be generic if it is satisfied on a residual set. By slight abuse of language, we use the term generic diffeomorphisms: the phase ‘generic diffeomorphisms satisfy property $P$ ‘ means that property $P$ is generic.

Let $f \in \mbox{Diff}^1(M)$ be a diffeomorphism of $M$ . For all $\varepsilon>0$ , an $\varepsilon$ -pseudo-orbit of $f$ is a sequence (finite or infinite) of points $(x_i)$ such that for all $i$ , $d(x_{i+1},f(x_i)) < \varepsilon$ . We define the following binary relations for pairs of points $(x,y)$ on $M$ :

– For all $\varepsilon > 0$ , we write $x \dashv_\varepsilon y$ if there exists an $\varepsilon$ -pseudo-orbit $(x_0, x_1, \cdots, x_k)$ where $x_0 = x$ and $x_k = y$ for some $k \geq 1$ .

– We write ${x \dashv y}$ if ${x \dashv_\varepsilon y}$ for all ${\varepsilon>0}$ . We sometimes write ${x \dashv_f y}$ to specify the dynamical system in consideration.

– We write ${x \prec y}$ (or ${x \prec_f y}$ ) if for all neighborhoods ${U, V}$ of ${x}$ and ${y}$ , respectively, there exists ${n \geq 1}$ such that ${f^n(U)}$ intersects ${V}$ .

Here are a few elementary properties of these relations.

1. The relations ${\dashv}$ and ${\dashv_\varepsilon}$ are, by construction, transitive. The chain recurrent set ${\mathcal{R}(f)}$ is the set of points ${x}$ in ${M}$ such that ${x \dashv x}$ .

2. The relation ${x \prec y}$ is not a-priori transitive. The non-wandering set ${\Omega(f)}$ is the set of points ${x}$ in ${M}$ such that ${x \prec x}$ .

Marie-Claude Arnaud has shown in [Ar] that the relation ${\prec}$ is transitive for generic diffeomorphisms. By using similar methods we show:

Theorem 1: There exists a residual set ${\mathcal{G}}$ in ${\mbox{Diff}^1(M)}$ (or in ${\mbox{Diff}^1_\omega(M)}$ ) such that for all diffeomorphisms ${f}$ in ${\mathcal{G}}$ and all pair of points ${(x, y)}$ in ${M}$ we have:

$\displaystyle x \dashv_f y \Longleftrightarrow x \prec_f y.$

This theorem is a consequence of the following general perturbation result:

Theorem 2: Let ${f}$ be a diffeomorphism on compact manifold ${M}$ , satisfying one of the following two hypotheses:

1. all periodic orbits of ${f}$ are hyperbolic,

2. ${M}$ is a compact surface and all periodic orbits are either hyperbolic or elliptic with irrational rotation number (its derivative has complex eigenvalues, all of modulus ${1}$ , but are not powers of roots of unity).

Let ${\mathcal{U}}$ be a ${C^1}$ -neighborhood of ${f}$ in ${\mbox{Diff}^1(M)}$ (or in ${\mbox{Diff}^1_\omega(M)}$ , if ${f}$ preserves volume form ${\omega}$ ). Then for all pairs of points ${(x,y)}$ in ${M}$ such that ${x \dashv y}$ , there exists a diffeomorphism ${g}$ in ${\mathcal{U}}$ and an integer ${n>0}$ such that ${g^n(x) = y}$ .

Remark: In Theorem 2 above, if the diffeomorphism ${f}$ if of class ${C^r}$ with ${r \in (\mathbb{N} \backslash \{0\})\cup \{ \infty \}}$ , then the ${C^1}$ -perturbation ${g}$ can also be chosen in class ${C^r}$ . Indeed the diffeomorphism ${g}$ is obtained thanks to a finite number of ${C^1}$ -perturbations given by the connecting lemma (Theorem 2.1), each of these perturbations is itself of class ${C^r}$ .

Here are a few consequences of these results:

Corollary: There exists a residual set ${\mathcal{G}}$ in ${\mbox{Diff}^1(M)}$ such that for all diffeomorphism ${f}$ in ${\mathcal{G}}$ , the chain recurrent set ${\mathcal{R}(f)}$ coincides with the non-wandering set ${\Omega(f)}$ .

Corollary: Suppose ${M}$ is connected, then there exists a residual set ${\mathcal{G}}$ in ${\mbox{Diff}^1(M)}$ such that if ${f \in \mathcal{G}}$ satisfies ${\Omega(f) = M}$ then it is transitive. Furthermore, ${M}$ is the unique homoclinic class for ${f}$ .

For volume preserving diffeomorphism ${f}$ , the set ${\Omega(f)}$ always coincide with the whole manifold ${M}$ . We therefore find the analogue of this corollary in the conservative case (see section 1.2.4).

2. Dynamical decomposition of generic diffeomorphisms into elementary pieces

Consider the symmetrized relation ${\vdash\dashv }$ of ${\dashv}$ defined by ${x \vdash\dashv y}$ if ${x \dashv y}$ and ${y\dashv x}$ . This relation then induces an equivalence relation on ${\mathcal{R}(f)}$ , where the equivalence classes are called chain recurrence classes.

We say a compact ${f}$ -invariant set ${\Lambda}$ is weakly transitive if for all ${x, y \in \Lambda}$ , we have ${x \prec y}$ . A set ${\Lambda}$ is maximally weakly transitive if it is maximal under the partial order ${\subseteq}$ among the collection of weakly transitive sets.

Since the closure of increasing union of weakly transitive sets is weakly transitive, Zorn’s lemma implies any weakly transitive set is contained in a maximally weakly transitive set. In the case where the relation ${\prec_f}$ is transitive (which is a generic property), the maximally weakly transitive sets are the equivalence classes of the symmetrized relation induced by ${\prec}$ on the set ${\Omega(f)}$ . Hence we obtain, for generic diffeomorphisms:

Corollary: There exists residual set ${\mathcal{G}}$ in ${\mbox{Diff}^1(M)}$ such that for all ${f \in \mathcal{G}}$ the chain recurrence classesare exactly the maximally weakly transitive sets of ${f}$ .

The result of Conley (see posts on fundamental theorem of dynamical systems) on the decomposition of ${\mathcal{R}(f)}$ into chain recurrence classes will therefore apply (for generic diffeomorphisms) to the decomposition of ${\Omega(f)}$ into maximally weakly transitive sets.

${\cdots}$

3. Chain recurrence classes and periodic orbits

Recall that after the establishment of closing lemma by C. Pugh (see the closing lemma post), it is known that periodic points are dense in ${\Omega(f)}$ for generic diffeomorphisms, we would like to use these periodic orbits to better understand the dynamics of chain recurrence classes.

Recall the homoclinic class ${H(p, f)}$ of a hyperbolic periodic point ${p}$ is the closure of all transversal crossing points of its stable and unstable manifolds. This set is by construction transitive, as we have seen in section 1.2, the results of [CMP] imply that, for generic diffeomorphisms any homoclinic class is maximally weakly transitive. By applying corollary 1.4, we see that:

Remark: For generic diffeomorphisms homoclinic classes are also chain recurrence classes.

However, for generic diffeomorphisms, there are chain recurrence classes which are not homoclinic classes, therefore contains no periodic orbit, we call such chain recurrence class with no periodic points aperiodic class.

Corollary: There exists residual set ${\mathcal{G}}$ in ${\mbox{Diff}^1(M)}$ such that for all ${f \in \mathcal{G}}$ , any connected component with empty interior of ${\Omega(f) = \mathcal{R}(f)}$ is periodic and its orbit is a homoclinic class.

The closing lemma of Pugh and Remark 5 show:

Remark: For generic ${f}$ , any isolated chain recurrence class in ${R(f)}$ is a homoclinic class. In particular this applies to classes that are topological attractors or repellers.
${\cdots}$

For non-isolated classes, a recent work (see [Cr]) specifies how a chain recurrence class is approximated by periodic orbits:

Theorem: There exists residual set ${\mathcal{G}}$ in ${\mbox{Diff}^1(M)}$ such that for all ${f \in \mathcal{G}}$ , all maximally weakly transitive sets of ${f}$ are Hausdorff limits of sequences of periodic orbits.

More general chain recurrence classes satisfy the upper semi-continuity property: if ${(x_i) \subseteq \mathcal{R}(f)}$ is a sequence of points converging to a point ${x}$ then for large enough ${n}$ , the class of ${x_n}$ is contained in an arbitrary small neighborhood of the class of ${x}$ .

C^1 vs. C^1 volume preserving

January 23, 2011February 28, 2011 Conan4 Comments

One of the things I’ve always been interested in is, for a given compact set say in $\mathbb{R}^n$ , what maps defined on the set into $\mathbb{R}^n$ can be extended to a volume preserving map (of certain regularity) on a larger set (for example, some open set containing the original set).

The analogues extension question without requiring the extended map to be volume preserving is answered by the famous Whitney’s extension theorem. It gives a beautiful necessary and sufficient condition on when the map has $C^r$ extension – See this pervious post for more details.

A simple case of this type of question was discussed in my earlier Moser’s theorem post:

Question: Given a diffeomorphism on the circle, when can we extend it to a volume preserving diffeomorphism on the disc?

In the post, we showed that any $C^r$ diffeomorphism on the circle can be extended to a $C^{r-1}$ volume preserving diffeomorphism on the disc. Some time later Amie Wilkinson pointed out to me that, by using generating function methods, in fact one can avoid losing derivative and extend it to a $C^r$ volume preserving.

Anyways, so we know the answer for the circle, what about for sets that looks very different from the circle? Is it true that whenever we can $C^r$ extend the map, we can also so it volume-preserving? (Of course we need to rule out trivial case such as the map is already not volume-preserving on the original set or the map sends, say a larger circle to a smaller circle.)

Question: Is it true that for any compact set $K \subseteq \mathbb{R}^n$ with connected complement, for any function $f: K \rightarrow \mathbb{R}^n$ satisfying the Whitney condition with all candidate derivatives having determent $1$ , one can always extend $f$ to a volume preserving $F: \mathbb{R}^n \rightarrow \mathbb{R}^n$ .

Note: requiring the set to have connected complement is to avoid the ‘larger circle to small circle’ case and if some candidate derivative does not have determent $1$ then the extended map cannot possibly be volume preserving near the point.

After thinking about this for a little bit, we (me, Charles and Amie) came up with the following simple example where the map can only be $C^1$ extended but not $C^1$ volume preserving.

Example: Let $K \subset \mathbb{R}^2$ be the countable union of segments:

$K = \{0, 1, 1/2, 1/3, \cdots \} \times [0,1]$

As shown below:

Define $f: K \rightarrow K$ be the map that sends the vertical segment above $1/n$ to the vertical segment above $1/(n+1)$ , preserves the $y$ -coordinate and fixes the segment $\{0\} \times [0,1]$ :

Claim: $f$ can be extended to a $C^1$ map $F: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ .

Proof: Define $g: \mathbb{R} \rightarrow \mathbb{R}$ s.t.

1) $g$ is the identity on $\mathbb{R}^{\leq 0}$

2) $g(x) = x-1/2$ for $x>1$

3) $g: 1/n \mapsto 1/(n+1)$

4) $g$ is increasing and differentiable on each $[1/n, 1/(n-1)]$ with derivative no less than $(1-1/n)(n^2-n)/(n^2+n)$ and the one sided derivative at the endpoints being $1$ .

It’s easy to check such $g$ exists and is continuous:

Since $\lim_{n \rightarrow \infty} (1-1/n)(n^2-n)/(n^2+n) = 1$ , we deduce $g$ is continuously differentiable with derivative $1$ at $0$ .

Let $F = g \otimes \mbox{id}$ , $F: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ is a $C^1$ extension of $f$ .

Establishes the claim.

Hence the pair $(K, f)$ satisfies the Whitney condition for extending to $C^1$ map. Furthermore, since the $F$ as above has derivative being the identity matrix at all points of $K$ , the determent of candidate derivatives are uniformly $1$ . In other words, this example satisfies all conditions in the question.

Claim: $f$ cannot be extended to a $C^1$ volume preserving diffeomorphism of the plane.

Proof: The idea here is to look at rectangles with sides on the set $K$ , if $F$ preserves area, they have to go to regions enclosing the same area as the original rectangles, then apply the isoperimetric inequality to deduce that image of some edges of the rectangle would need to be very long, hence at some point on the edge the derivative of $F$ would need to be large.

Suppose such extension $F$ exists, consider rectangle $R_n = [1/n, 1/(n-1)] \times [0,1]$ . We have

$m_2(R_n) = 1/(n^2-n)$

$m_2(R_n) - m_2(R_{n+1})$

$=1/(n^2-n)-1/(n^2+n)=2/(n^3-n)$

Hence in order for $F(R_n)$ to have the same area as $R_n$ , the image of the two segments

$s_{n,0} = [1/n, 1/(n-1)] \times \{ 0\}$ and

$s_{n,1}= [1/n, 1/(n-1)] \times \{ 1\}$

would need to enclose an area of $2/(n^3-n) \sim n^{-3}$ outside of the rectangle $R_{n+1}$ .

By isoparametric inequality, the sum of the length of the two curves must be at least $\sim n^{-3/2}$ , while the length of the original segments is $2/(n^2-n) \sim n^{-2}$ .

Hence somewhere on the segments $F$ needs to have derivative having norm at least

$\ell(F(s_{n,0} \cup s_{n,1}) / \ell(s_{n,0} \cup s_{n,1})$

$\sim n^{-3/2}/n^{-2} = n^{1/2}$

We deduce that there exists a sequence of points $(p_n)$ converging to either $(0,0)$ or $(0,1)$ where

$|| F'(p_n) || \sim n^{1/2} \rightarrow \infty$ .

Hence $F$ cannot be $C^1$ at the limit point of $(p_n)$ .

Remark: In fact we have showed the stronger statement that no volume preserving Lipschitz extension could exist and gave an upper bound $1/2$ on the best possible Holder exponent.

From this we know the answer to the above question is negative, i.e. not all $C^1$ extendable map can me extended in a volume preserving fashion. It would be very interesting to give criteria on what map on which sets can be extended. By applying same methods we are also able to produce an example where the set $K$ is a Cantor set on the plane.

A convergence theorem for Riemann maps

January 17, 2011November 1, 2011 ConanLeave a comment

So~ After 2.5 weeks of wonderful math discussions with Amie and Charles, I finished my winter vacation and got back to Princeton! (and back to my normal blogging Sundays ^^)

One thing I would like to shear here is that we (me and Charles) finally got an answer to the following question that’s been haunting me for a while:

Question: Given Jordan curve $C \subseteq \mathbb{C}$ containing a neighborhood of $\bar{0}$ in its interior. Given parametrizations $\gamma_1:S^1 \rightarrow C$ .

Is it true that for all $\varepsilon >0$ , there exists $\delta >0$ s.t. any Jordan curve $C'$ with a parametrization $\gamma_2:S^1 \rightarrow C_2$ so that $||\gamma_1-\gamma_2||<\delta$ in the uniform norm implies the Riemann maps $R, R'$ from $\mathbb{D}$ to the interiors of $C, C'$ that fixes the origin and have positive real derivatives at $\bar{0}$ would be at most $\varepsilon$ apart?

i.e. Is the projection map from the space of parametrized Jordan curves (with the uniform metric) to the space of unparametrized Jordan curves (with metric given by taking uniform distance between the canonical Riemann maps) continuous?

First, I think the development and problem-solving process for this one is quite interesting and worth mentioning (skip this if you just want to see math):

—Begin story—

The problem was initially of interest because I stated a lemma on our Jordan curves paper which asserts the above projection map is continuous at smooth curves. To my surprise, I was unable to prove this seemingly-direct lemma. I turned to Charles for help, after a day or so of thinking he proved it for smooth curves (via a very clever usage of cross-cuts as in the proof of Carathedory’s theorem) and asked back whether the map is actually continuous at all points.

This seemed to be such a natural question but we couldn’t find it in the literature. For a day or so we were both feeling negative about this since the cross-cut method fails when the Jordan curve has positive measure, which “should” happen a lot. In any case, I posted a question on mathoverflow to see if there is a standard theorem out there implying this. Almost right after I posted the question, during a wonderful lunch-conversation with Charles, I got this wonderful idea of applying extremal length techniques not to the semi-circular crosscut but only to the ‘feet’ of it. Which later that day turned out to be a proof of the continuity.

The next morning, after confirming the steps of the proof and made sure it works, I was thrilled to find that Thurston responded to the post and explained his intuition that the answer is positive. Although having solved the problem already, I am still amazed by his insights ^^ (It’s the second question I asked there, he left an comment again! It just feels great to have your idol giving you ideas, isn’t it? :-P)

Later on, McMullen pointed out to us that in fact a book by Pommerenke contains the result. Nevertheless, it was great fun proving this, hence I decided to sketch the proof here ^^

—End story—

Ingredients of the proof: We quote the following well-known but weaker theorem (one can find this in, for example Goluzin’s classical book, p228)

Theorem: If the Jordan domains converge (in the sense that parametrizations of the boundaries converge uniformly) then the Riemann maps converge uniformly on compact sets.

We also use the following topological lemma:

Lemma: Given Jordan curve $C \subseteq \hat{\mathbb{C}}$ , $\gamma: S^1 \rightarrow C$ be a parametrization. For all $\varepsilon > 0$ , there exists $\mu >0$ s.t. for all $\gamma' : S^1 \rightarrow \hat{\mathbb{C}}$ with $|| \gamma - \gamma'|| < \mu$ ( denote C' = \gamma'(S^1)$) , for all $p, q \in C'$ , $d(p,q) < \mu \Rightarrow \mbox{diam}(A(p,q)) < \varepsilon$

where $A(p,q)$ is the short arc in $C'$ connecting $p, q$ .

The proof of the lemma is left as an exercise

Proof of the Theorem:

Given $C$ and $\varepsilon$ as in the theorem, apply the lemma to $(C, \varepsilon/6)$ , we obtain a $\mu < \varepsilon / 6$ so that all curves $\mu$ -close to $C$ has the property that the arc connecting any two points less than $\mu$ -apart has diameter no more than $\varepsilon/100$ .

By compactness of $\partial \mathbb{D}$ , we can choose finitely many crosscut neignbourhoods $\{ H_1, H_2, \cdots, H_N \}$ , $H_i \subseteq \bar{\mathbb{D}}$ are "semi-discs" around points in $\partial \mathbb{D}$ as shown:

By extremal length, we can choose the cross-cuts $C_i$ bounding $H_i$ with length $\ell(R(C_i)) < \mu/4$ where $R: \bar{\mathbb{D}} \rightarrow \hat{\mathbb{C}}$ is the canonical Riemann map corresponding to $C$ . Hence by lemma, we also get $\mbox{diam}(R(H_i) < \varepsilon/3$ .

Let $\{ f_1, f_2, \cdots, f_{2N} \}$ be endpoints of $\{C_1, \cdots, C_N \}$ .

Let $d = \min \{ d(f_i, f_j) \ | \ 1 \leq i < j \leq 2N \}$ .

Choose $\sigma < \mu d / 40$ and $\{ B( \bar{0}, 1-2\sigma), H_1, \cdots, H_N \}$ covers $\bar{\mathbb{D}}$ . Let $R = 1-\sigma$ :

By the above theorem in Goluzin, since $B_R = \bar{B(0, R)}$ is compact, there exists a $0 < \delta < \min \{\mu/4, d/10 \}$ s.t.

$|| \gamma' - \gamma || < \delta$ $\Rightarrow ||R|_{B_R} - R'|_{B_R}|| < \mu/4$ .

Fix a $(C', \gamma')$ with $|| \gamma - \gamma'|| < \delta$ . Let $R'$ be the canonical Riemann map corresponding to $C'$ .

Claim: $||R-R'|| < \varepsilon$ .

First note that assuming the theorem in Goluzin, it suffice to show $||R|_{\partial \mathbb{D}} - R'|_{\partial \mathbb{D}}|| < \varepsilon$ .

For any $1 \leq i \leq N$ , let $f_1, f_2$ be endpoints of $C_i$ . Apply the extremal length to the set of radial segments in the almost-rectangle $[f_1, f_1+d/10] \times [0,\sigma]$ .

We conclude there exists $e_1 \in [f_1, f_1+d/10]$ s.t. the segment $s_1 = \{e_1\} \times [0, \sigma]$ has length

$\ell(R'(s_1)) \leq 2 \sigma (d/10) m_2(R'([f_1, f_1+d/10] \times [0,\sigma]))$ .

Since $\sigma < \mu d / 40$ and $m_2(R'([f_1, f_1+d/10] \times [0,\sigma])) \leq 1$ , we have

$\ell(R'(s_1)) \leq \mu/4$ .

Similarly, find $e_2 \in [f_2 - d/10, f_2]$ where $\ell(R'(s_2)\leq \mu/4$ .

Connect $e'_1, e'_2$ by a semicircle contained in $H_i$ , denote the enclosed region by $V_i \subseteq H_i$ .

By construction, $\{ B_R, V_1, \cdots, V_N \}$ still covers $\bar{\mathbb{D}}$ .

Hence for all $p \in \partial \mathbb{D}$ , there exists $i$ where $p \in$ latex V_i$.

Since inside $V_i \cap B_R$ the two maps $R, R'$ are less than $d/10$ apart, we have $R(V_i) \cap R'(V_i) \neq \phi$ .

Hence $d(R(p), R'(p)) \leq \mbox{diam}(R(H_i)) + \mbox{diam}(R'(V_i))$ .

By construction, $\mbox{diam}(R(H_i)) < \varepsilon/2$ .

$\mbox{diam}(R'(V_i)) = \mbox{diam}(\partial V_i)$ , we will break $\partial V_i$ into three parts and estimate diameter of each part separately.

Since $||\gamma-\gamma'|| < \delta$ , $\tau = \gamma' \circ \gamma^{-1} \circ R|_{\partial \mathbb{D}}$ is another parametrization of $C'$ with $|| \tau - R|_{\partial \mathbb{D}}|| < \delta$ .

The arc connecting $e'_1$ to $e'_2$ is contained in $B_R \cap V_i$ , the arc in $C'$ connecting $\tau(e_1), \tau(e_2)$ is $\delta$ away from $R(H_i)$ hence the union of the two has diameter at most $\mbox{diam}(R(V_i)) + \delta < \varepsilon/6 + \varepsilon/6 = \varepsilon/3$

Length of the arcs $R'(s_1), R'(s_2)$ are less than $\mu/4 < \varepsilon/12$ .

Hence $d(\tau(e_1), R'(e_1)) < \ell(R'(s_1)) + \delta < \mu$ . By lemma, this implies the arc in $C'$ connecting $\tau(e_1), R'(e_1)$ has length at most $\varepsilon/12$ .

Hence altogether the we have $\mbox{diam}(R'(V_i)) \leq \varepsilon/3+\varepsilon/12+\varepsilon/12 = \epsilon/2$ .

We deduce $d(R(p), R'(p)) \leq \mbox{diam}(R(H_i)) + \mbox{diam}(R'(V_i)) < \varepsilon$ .

Q.E.D.

Area777

Chasing dreams from mathematics to the real world

Tag: Charles Pugh

The Carnot-Carathéodory metric

A survey on ergodicity of Anosov diffeomorphisms

Recurrence and genericity – a translation from French

C^1 vs. C^1 volume preserving

A convergence theorem for Riemann maps

Share this:

Share this:

Share this:

Share this:

Share this: