Tag: Larry Guth

The travelling salesman problem

ConanLeave a comment

This is one of those items I should have written about long ago: I first heard about it over a lunch chat with professor Guth; then I was in not one, but two different talks on it, both by Peter Jones; and now, finally, after it appeared in this algorithms lecture by Sanjeev Arora I happen to be in, I decided to actually write the post. Anyways, it seem to live everywhere around my world, hence it’s probably a good idea for me to look more into it.

Has everyone experienced those annoy salesman who keeps knocking on you and your neighbors’ doors? One of their wonderful properties is that they won’t stop before they have reached every single household in the area. When you think about it, in fact this is not so straight foreword to do; i.e. one might need to travel a long way to make sure each house is reached.

Problem: Given N points in \mathbb{R}^2, what’s the shortest path that goes through each point?

Since this started as an computational complexity problem (although in fact I learned the analysts’s version first), I will mainly focus on the CS version.

Trivial observations:

In total there are about N! paths, hence the naive approach of computing all their lengths and find the minimum takes more than N! \sim (N/e)^N time. (which is a long time)

This can be easily improved by a standard divide and concur:

Let V \subseteq \mathbb{R}^2 be our set of points. For each subset S \subseteq V, for each p_1, p_2 \in S, let F(S, p_1, p_2) = length of shortest path from p_1 to p_2 going through all points in S.

Now the value of this F can be computed recursively:

\forall |S| = 2, F(S, p_1, p_2) = d(p_1, p_2);

Otherwise F(S, p_1, p_2) =

\min \{ F(S \backslash \{p_2\}, p_1, q) + d(q, p_2) \ | \ q \in S, q \neq p_1, p_2 \}

What we need is minimum of F(V, p_1, p_2) where p_1, p_2 \in V. There are 2^N subsets of V, for any subset there are \leq N choices for each of p_1, p_2. F(S, p_1, p_2) is a minimum of N numbers, hence O(N) time (as was mentioned in this pervious post for selection algorithm). Summing that up, the running time is 2^N\times N^2\times N \sim O(2^N), slightly better than the most naive way.

Can we make it polynomial time? No. It’s well known that this problem is NP-hard, this is explained well in the wikipedia page for the problem.

Well, what can we do now? Thanks to Arora (2003), we can do an approximate version in polynomial time. I will try to point out a few interesting ideas from that paper. The process involved in this reminded me of the earlier post on nonlinear Dvoretzky problem (it’s a little embracing that I didn’t realize Sanjeev Arora was one of the co-authors of the Dvoretzky paper until I checked back on that post today! >.< ) it turns out they have this whole program about ‘softening’ classic problems and produce approximate versions.

Approximate version: Given N points in \mathbb{R}^2, \forall \varepsilon > 0, find a path \gamma through each point such that length l(\gamma) < (1+\varepsilon)l(\mbox{Opt}).

Of course we shall expect the running time T to be a function of \varepsilon and N, as \varepsilon \rightarrow 0 it shall blow up (to at least exponential in N, in fact as we shall see below, it will blow up to infinity).

The above is what I would hope is proved to be polynomial. In reality, what Arora did was one step more relaxed, namely a polynomial time randomized approximate algorithm. i.e. Given V and \varepsilon, the algorithm produces a path \gamma such that E(l(\gamma)-l(\mbox{Opt}) < \varepsilon). In particular this means more than half the time the route is within (1+\varepsilon) to the optimum.

Theorem (Arora ’03): T(N, \varepsilon) \sim O(N^{1/\varepsilon}) for the randomized approximate algorithm.

Later in that paper he improved the bound to O(N \varepsilon^{C/\varepsilon}+N\log{N}), which remains the best know bound to date.

Selected highlights of proof:

One of the great features in the approximating world is that, we don’t care if there are a million points that’s extremely close together — we can simply merge them to one point!

More precisely, since we are allowing a multiplicative error of \varepsilon, we also have trivial bound l(\mbox{Opt}) > \mbox{ diam}(V), Hence the length can be increased by at least \varepsilon \mbox{diam}(V) which means if we move each point by a distance no more than \varepsilon \mbox{diam}(V) / (4N) and produce a path \gamma' connecting the new points with l(\gamma')< (1+\varepsilon/2)l(\mbox{Opt}), then we can simply get our desired \gamma from \gamma', as shown:

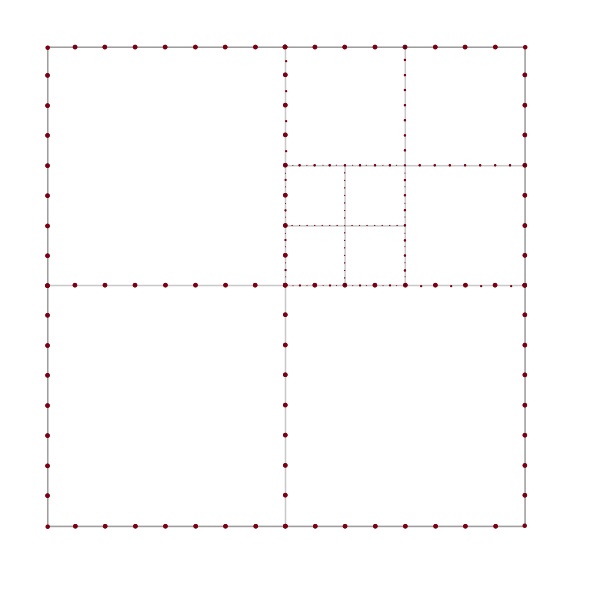
i.e. the problem is “pixelated”: we may bound V in a square box with side length \mbox{diam}(V), divide each side into 8N/\varepsilon equal pieces and assume all points are in the center of the gird cell it lies in (for convenience later in the proof we will assume 8N/\varepsilon = 2^k is a power of 2, rescale the structure so that each cell has side length 1. Now the side length of the box is 8N/\varepsilon = 2^k):

Now we do this so-called quadtree construction to separate the points (reminds me of Whitney’s original proof of his extension theorem, or the diatic squares proof of open sets being countable) i.e. bound V in a square box and keep dividing squares into four smaller ones until no cell contains more than one point.

In our case, we need to randomize the quad tree: First we bound V in a box that’s 4 times as large as our grid box (i.e. of side length 2^{k+1}), shift the larger box by a random vector (-i/2^k,-j/2^k) and then apply the quad tree construction to the larger box:

At this point you may wonder (at least I did) why do we need to pass to a larger square and randomize? From what I can see, doing this is to get

Fact: Now when we pick a grid line at random, the probability of it being an ith level dividing line is 2^i/2^k = 2^{i-k}.

Keep this in mind.

Note that each site point is now uniquely defined as an intersection of no more than k nesting squares, hence the total number of squares (in all levels) in this quad tree cannot exceed N \times k \sim N \times \log{N/\varepsilon}.

Moving on, the idea for the next step is to perturb any path to a path that cross the sides of the square at some specified finite set of possible “crossing points”. Let m be the unique number such that 2^m \in [(\log N)/\varepsilon, 2 (\log N)/ \varepsilon ] (will see this is the best m to choose). Divide sides of each square in our quad tree into 2^m equal segments:

Note: When two squares of different sizes meet, since the number of equally squares points is a power of 2, the portals of the larger square are also portals of the smaller one.

With some simple topology (! finally something within my comfort zone :-P) we may assume the shortest portal-respecting path crosses each portal at most twice:

In each square, we run through all possible crossing portals and evaluate the shortest possible path that passes through all sites inside the square and enters and exists at the specified nodes. There are (2^{4 \times 2^m})^2 \sim (side length)^2 \sim (N/\varepsilon)^2 possible entering-exiting configurations, each taking polynomial time in N (in fact \sim N^{O(1/\varepsilon)} time) to figure out the minimum.

Once all subsquares has their all paths evaluated, we may move to the one-level larger square and spend another \log(N/\varepsilon) \times (N/\varepsilon)^2 operations. In total we have

N \times \log{N/\varepsilon} \times (N/\varepsilon)^2 \times N^{O(1/\varepsilon)}

\sim N^{O(1/\varepsilon)}

which is indeed polynomial in N/\varepsilon many operations.

The randomization comes in because the route produced by the above polynomial time algorithm is not always approximately the optimum path; it turns out that sometimes it can be a lot longer.

Expectation of the difference between our random portal respecting minimum path \mbox{OPT}_p and the actual minimum \mbox{OPT} is bounded simply by the fact that minimum path cannot cross the grid lines more that \mbox{OPT} times. At each crossing, the edge it crosses is at level i with probability 2^{i-k}. to perturb a level i intersection to a portal respecting one requires adding an extra length of no more than 2 \times 2^{k-i}/2^m \sim 2^{k+1-i}/(\log N / \varepsilon):

\displaystyle \mathbb{E}_{a,b}(\mbox{OPT}_p - \mbox{OPT})

\leq \mbox{OPT} \times \sum_{i=1}^k 2^{i-k} \times 2^{k+1-i} / (\log N / \varepsilon)

= \mbox{OPT} \times 2 \varepsilon / \log N < \varepsilon \mbox{OPT}

P.S. You may find images for this post being a little different from pervious ones, that’s because I recently got myself a new iPad and all images above are done using iDraw, still getting used to it, so far it’s quite pleasant!

Bonus: I also started to paint on iPad~

–Firestone library, Princeton. (Beautiful spring weather to sit outside and paint from life!)

A Bosuk-Ulam-kind theorem for simplexes

Conan1 Comment

This little note came out of a lunch discussion with NYU grad student Alfredo Hubard earlier this week. I think the problem-solving process was quite amusing hence worth shearing.

Back in kindergarten, we all learned this theorem called ‘at any given time, there are two opposite places on Earth having exactly the same temperature and air pressure’. Yes that’s the Bosuk-Ulam theorem. I remember at some point I came across a much less famous theorem in some kind of discrete/combinatorial geometry, saying:

Theorem: Any map from a n-dimensional simplex to \mathbb{R}^{n-1} must have a pair of intersecting opposite faces.

Note: each k-dimensional face of the n-dimensional simplex has a unique, well-defined (n-1)-k dimensional opposite face, as shown:

Some examples of maps from the 3-simplex to \mathbb{R}^2:

i.e. in general they can be quite a mess. I think it can be proved by Thurston’s simplex straightening argument. (haven’t checked carefully)

To me this is like Bosuk-Ulam except for instead of considering a large amount of antipodal pairs, we consider only finitely many such pairs. Hence a discrete analoge.

However, one should note that although they are of the same nature, neither follows from the other.

So somehow this theorem came up during the lunch and Alfredo mentioned to me that professor Guth wondered whether the theorem can be proved for mappings from the simplex to lower dimensional simplicial complexes (instead of \mathbb{R}^n). i.e.

Question: Given f: \Delta^{n+1} \rightarrow S where \Delta^{n+1} denote the (n+1)-dimensional simplex and S is a n-dimensional simplicical complex. Then must there be a pair of opposite faces with intersecting image?

So we started to throw out random ideas.

First of all, although only boundary faces of the simplex has non-empty opposite faces (hence can possibly be intersecting pair), it is important that f: \Delta^n \rightarrow S is defined on the solid simplex. (i.e. if one just map the boundary, then we may let S be topologically a sphere and make the map a homeomorphism!) So the moral is, we kind of need to ‘claps’ the simplex to a simply connected lower dimensional thing first, then map it to our S, hence S having non-trivial topology won’t be of much help. Looks almost like the \mathbb{R}^n case, doesn’t it?

Perhaps the image on S can be complicated and has non-trivial topology, but this is merely ‘wrapping’ a contractible, n-dimensional thing around. But wrapping around can only cause more overlapping hence making the faces intersecting more, not less.

The above line of thoughts give an immediate proof in the case when S is a surface and n=2: Lift the map to the universal cover and apply the theorem for \mathbb{R}^2. (It’s a little more tricky when the surface is \mathbb{S}^2 but you can work it out~ the map restricted to \partial \Delta must be of even degree) Note this won’t generalize to higher dimensions (even for manifolds) since universal covers are no longer that similar to \mathbb{R}^n.

So what’s the main difference between complexes and manifolds? well, one can have more than two n dimensional faces attached to the same n-1 dimensional face. I decided to first think of whether Bosuk-Ulam is still true if we further assume that the map extends to the solid ball (as seen above, it is true in the surface case).

After trying to generalize that ‘lifting’ proof for a while, we realized the Bosuk-Ulam does not work for simplicial complexes in all dimensions! For very simple reason, i.e. if we map the n-sphere to \mathbb{R}^n by projecting down, the pre-image of the center point is the only pair of antipodal points that’s mapped together. Hence if instead of \mathbb{R}^n we have three n-simplicies attached along a single (n-1)-simplex (think of it as a piece of \mathbb{R}^n with a vertical simplex attached in the middle):

Now we can still project to that piece of \mathbb{R}^n, with the image of antipodal point lying on the middle (n-1) simplex, all we need to do is to separate this pair while not creating new pairs! But this is easy, just ‘drug’ the upper sheet into the third n-simplex a little bit:

(the region outside of the red neibourhood is unchanged) It’s easy to see that no new antipodal pair is moved together.

So now we turned back to the simplex and realized it’s even easier to argue: project in orthogonal direction to a n-face, originally the only intersecting pair of opposite faces was the vertex and that n-face. Now if we lift the vertex int the third sheet, nothing can intersect~

OK~ perhaps not a useful answer but problem solved!

So far I do not know the answer to the following:

Questions:

1. Is this intersecting faces theorem true for mapping n-simplexes to n-dimensional manifolds?

2. Is the Bosuk-Ulam true if we consider maps from spheres to n-dimensional manifolds which extends to the ball?

The later might be well-known. But so far I can only find a theorem by Conner and Floyd, stating that any map from S^n to a lower dimensional manifold must have a pair of antipodal points mapped together.

A report of my Princeton generals exam

ConanLeave a comment

Well, some people might be wondering why I haven’t updated my blog since two weeks ago…Here’s the answer: I have been preparing for this generals exam — perhaps the last exam in my life.

For those who don’t know the game rules: The exam consists of 3 professors (proposed by the kid taking the exam, approved by the department), 5 topics (real, complex, algebra + 2 specialized topics chosen by the student). One of the committee member acts as the chair of the exam.

The exam consists of the three committee members sitting in the chair’s office, the student stands in front of the board. The professors ask questions ranging in those 5 topics for however long they want, the kid is in charge of explaining them on the board.

I was tortured for 4.5 hours (I guess it sets a new record?)
I have perhaps missed some questions in my recollection (it’s hard to remember all 4.5 hours of questions).

Conan Wu’s generals

Commitee: David Gabai (Chair), Larry Guth, John Mather

Topics: Metric Geometry, Dynamical Systems

Real analysis:

Mather: Construct a first category but full measure set.

(I gave the intersection of decreasing balls around the rationals)

Guth: F:S^1 \rightarrow \mathbb{R} 1-Lipschitz, what can one say about its Fourier coefficients.

(Decreasing faster than c*1/n via integration by parts)

Mather: Does integration by parts work for Lipschitz functions?

(Lip imply absolutely continuous then Lebesgue’s differentiation theorem)

Mather: If one only has bounded variation, what can we say?

(f(x) \geq f(0) + \int_0^x f'(t) dt)

Mather: If f:S^1 \rightarrow \mathbb{R} is smooth, what can you say about it’s Fourier coefficients?

(Prove it’s rapidly decreasing)

Mather: Given a smooth g: S^1 \rightarrow \mathbb{R}, given a \alpha \in S^1, when can you find a f: S^1 \rightarrow \mathbb{R} such that
g(\theta) = f(\theta+\alpha)-f(\theta) ?

(A necessary condition is the integral of g needs to vanish,
I had to expand everything in Fourier coefficients, show that if \hat{g}(n) is rapidly decreasing, compute the Diophantine set \alpha should be in to guarantee \hat{f}(n) being rapidly decreasing.

Gabai: Write down a smooth function from f:\mathbb{R}^2 \rightarrow \mathbb{R} with no critical points.

(I wrote f(x,y) = x+y) Draw its level curves (straight lines parallel to x=-y)

Gabai: Can you find a such function with the level curves form a different foliation from this one?

(I think he meant that two foliations are different if there is no homeo on \mathbb{R}^2 carrying one to the other,
After playing around with it for a while, I came up with an example where the level sets form a Reeb foliation, and that’s not same as the lines!)

We moved on to complex.

Complex analysis:

Guth: Given a holomorphic f:\mathbb{D} \rightarrow \mathbb{D}, if f has 50 0s inside the ball B_{1/3}(\bar{0}), what can you say about f(0)?

(with a bunch of hints/suggestions, I finally got f(0) \leq (1/2)^{50} — construct polynomial vanishing at those roots, quotient and maximal modulus)

Guth: State maximal modulus principal.

Gabai: Define the Mobius group and how does it act on \mathbb{H}.

Gabai: What do the Mobius group preserve?

(Poincare metric)

Mather: Write down the Poincare metric, what’s the distance from \bar{0} to 1? (infinity)

(I don’t remember the exact distance form, so I tried to guess the denominator being \sqrt{1-|z|}, but then integrating from 0 to 1 does not “barely diverge”. Turns out it should be (1-|z|^2)^2.)

Gabai: Suppose I have a finite subgroup with the group of Mobius transformations acting on \mathbb{D}, show it has a global fixed point.

(I sketched an argument based on each element having finite order must have a unique fixed point in the interior of \mathbb{D}, if two element has different fixed points, then one can construct a sequence of elements where the fixed point tends to the boundary, so the group can’t be finite.)

I think that’s pretty much all for the complex.

Algebra:

Gabai: State Eisenstein’s criteria

(I stated it with rings and prime ideals, which leaded to a small discussion about for which rings it work)

Gabai: State Sylow’s theorem

(It’s strange that after stating Sylow, he didn’t ask me do anything such as classify finite groups of order xx)

Gabai: What’s a Galois extension? State the fundamental theorem of Galois theory.

(Again, no computing Galois group…)

Gabai: Given a finite abelian group, if it has at most n elements of order divisible by n, prove it’s cyclic.

(classification of abelian groups, induction, each Sylow is cyclic)

Gabai: Prove multiplicative group of a finite field is cyclic.

(It’s embarrassing that I was actually stuck on this for a little bit before being reminded of using the previous question)

Gabai: What’s SL_2(\mathbb{Z})? What are all possible orders of elements of it?

(I said linear automorphisms on the torus. I thought it can only be 1,2,4,\infty, but turns out there is elements of order 6. Then I had to draw the torus as a hexagon and so on…)

Gabai: What’s \pi_3(S^2)?

(\mathbb{Z}, via Hopf fibration)

Gabai: For any closed orientable n-manifold M, why is H_{n-1}(M) torsion free?

(Poincare duality + universal coefficient)

We then moved on to special topics:

Metric Geometry:

Guth: What’s the systolic inequality?

(the term ‘aspherical’ comes up)

Gabai: What’s aspherical? What if the manifold is unbounded?

(I guessed it still works if the manifold is unbounded, Guth ‘seem to’ agree)

Guth: Sketch a proof of the systolic inequality for the n-torus.

(I sketched Gromov’s proof via filling radius)

Guth: Give an isoperimetric inequality for filling loops in the 3-manifold S^2 \times \mathbb{R} where S^2 has the round unit sphere metric.

(My guess is for any 2-chain we should have

\mbox{vol}_1(\partial c) \geq C \mbox{vol}_2(c)

then I tried to prove that using some kind of random cone and grid-pushing argument, but soon realized the method only prove

\mbox{vol}_1(\partial c) \geq C \sqrt{\mbox{vol}_2(c)}.)

Guth: Given two loops of length L_1, L_2, the distance between the closest points on two loops is \geq 1, what’s the maximum linking number?

(it can be as large as c L_1 L_2)

Dynamical Systems:

Mather: Define Anosov diffeomorphisms.

Mather: Prove the definition is independent of the metric.

(Then he asked what properties does Anosov have, I should have said stable/unstable manifolds, and ergodic if it’s more than C^{1+\varepsilon}…or anything I’m familiar with, for some reason the first word I pulled out was structurally stable…well then it leaded to and immediate question)

Mather: Prove structural stability of Anosov diffeomorphisms.

(This is quite long, so I proposed to prove Anosov that’s Lipschitz close to the linear one in \mathbb{R}^n is structurally stable. i.e. the Hartman-Grobman Theorem, using Moser’s method, some details still missing)

Mather: Define Anosov flow, what can you say about geodesic flow for negatively curved manifold?

(They are Anosov, I tried to draw a picture to showing the stable and unstable and finished with some help)

Mather: Define rotation number, what can you say if rotation numbers are irrational?

(They are semi-conjugate to a rotation with a map that perhaps collapse some intervals to points.)

Mather: When are they actually conjugate to the irrational rotation?

(I said when f is C^2, C^1 is not enough. Actually C^1 with derivative having bounded variation suffice)

I do not know why, but at this point he wanted me to talk about the fixed point problem of non-separating plane continua (which I once mentioned in his class).

After that they decided to set me free~ So I wandered in the hallway for a few minutes and the three of them came out to shake my hand.

Graph, girth and expanders

Conan2 Comments

In the book “Elementary number theory, group theory and Ramanujan graphs“, Sarnak et. al. gave an elementary construction of expander graphs. We decided to go through the construction in the small seminar and I am recently assigned to give a talk about the girth estimate of such graphs.

Given graph (finite and undirected) G, we will denote the set of vertices by V(G) and the set of edges E(G) \subseteq V(G)^2. The graph is assumed to be equipped with the standard metric where each edge has length 1.

The Cheeger constant (or isoperimetric constant of a graph, see this pervious post) is defined to be:

\displaystyle h(G) = \inf_{S\subseteq V_G} \frac{|\partial S|}{\min\{|S|, |S^c|\}}

Here the notation \partial S denote the set of edges connecting an element in S to an element outside of S.

Note that this is indeed like our usual isoperimetric inequalities since it’s the smallest possible ratio between size of the boundary and size of the set it encloses. In other words, this calculates the most efficient way of using small boundary to enclose areas as large as possible.

It’s of interest to find graphs with large Cheeger constant (since small Cheeger constant is easy to make: take two large graphs and connect them with a single edge).

It’s also intuitive that as the number of edges going out from each vertice become large, the Cheeger constant will become large. Hence it make sense to restrict ourselves to graphs where there are exactly k edges shearing each vertex, those are called k-regular graphs.

If you play around a little bit, you will find that it’s not easy to build large k-regular graphs with Cheeger constant larger than a fixed number, say, 1/10.

Definition: A sequence of k-regular graphs (G_i) where |V_{G_i}| \rightarrow \infty is said to be an expander family if there exists constant c>0 where h(G_i) \geq c for all i.

By random methods due to Erdos, we can prove that expander families exist. However an explicit construction is much harder.

Definition: The girth of G is the smallest non-trivial cycle contained in G. (Doesn’t this smell like systole? :-P)

In the case of trees, since it does not contain any non-trivial cycle, define the girth to be infinity.

The book constructs for us, given pair p, q of primes where p is large (but fixed) and q \geq p^8, a graph (p+1)-regular graphX^{p,q} with

\displaystyle h(X^{p,q}) \geq \frac{1}{2}(p+1 - p^{5/6 + \varepsilon} - p^{1/6-\varepsilon})

where 0 < \varepsilon < 1/6.

Note that the bound is strictly positive and independent of q. Giving us for each p, (X^{p,q}) as q runs through primes larger than p^8 is a (p+1)-regular expander family.

In fact, this constructs for us an infinite family of expander families: a (k+1)-regular one for each prime k and the uniform bound on Cheeger constant gets larger as k becomes larger.

One of the crucial step in proving this is to bound the girth of the graph X^{p,q}, i.e. they showed that g(X^{p,q}) \geq 2 \log_p(q) and if the quadratic reciprocity (\frac{p}{q}) = -1 then g(X^{p,q}) \geq 4 \log_p(q) - \log_p(4). This is what I am going to do in this post.

Let \mathbb H ( \mathbb Z) be the set of quaternions with \mathbb Z coefficient, i.e.

\mathbb H ( \mathbb Z) = \{ a+bi+cj+dk \ | \ a,b,c,d \in \mathbb Z \}

Fix odd prime p, let

\Lambda' = \{ \alpha \in \mathbb H(\mathbb Z) \ | \ \alpha \equiv 1 (mod 2) \}

\cup \ \{\alpha \in \mathbb H(\mathbb Z) \ | \ N(\alpha) = p^n \ \mbox{and} \ \alpha \equiv i+j+k (mod 2) \}

where the norm N on \mathbb H(\mathbb Z) is the usual N(a+bi+cj+dk) = a^2 + b^2 +c^2+d^2.

\Lambda' consists of points with only odd first coordinate or points lying on spheres of radius \sqrt{p^n} and having only even first coordinate. One can easily check \Lambda' is closed under multiplication.

Define equivalence relation \sim on \Lambda' by

\alpha \sim \beta if there exists m, n \in \mathbb{N} s.t. p^m \alpha = \pm p^n \beta.

Let \Lambda = \Lambda' / \sim, let Q: \Lambda' \rightarrow \Lambda be the quotient map.

Since we know \alpha_1 \sim \alpha_2, \beta_1 \sim \beta_2 \Rightarrow \alpha_1\beta_1 \sim \alpha_2\beta_2, \Lambda carries an induced multiplication with unit.

In elementary number theory, we know that the equation a^2+b^2+c^2+d^2 = p has exactly 8(p+1) integer solutions. Hence the sphere of radius p in \mathbb H(\mathbb Z) contain 8(p+1) points.

In each 4-tuple (a,b,c,d) exactly one is of a different parity from the rest, depending on whether p\equiv1 or 3 (mod 4). Restricting to solutions where the first coordinate is non-negative, having different parity from the rest (in case the first coordinate is 0, we pick one of the two solutions \alpha, -\alpha to be canonical), this way we obtain exactly p+1 solutions.

Let S'_p = \{ \alpha_1, \bar{\alpha_1}, \cdots, \alpha_k, \bar{\alpha_k}, \beta_1, \cdots, \beta_l \} be this set of p+1 points on the sphere. Note that the \betas represent the solutions where the first coordinate is exactly 0.

Check that S'_p generates \Lambda'.

We have \alpha_i \bar{\alpha_i} = p and -\beta_j^2 = p. By definition S'_p \subseteq \Lambda' and Q is injective on S'_p. Let S_p = Q(S'_p).

Consider the Cayley graph \mathcal G (\Lambda, S_p), this is a (p+1)-regular graph. Since S_p generares \Lambda, \mathcal G (\Lambda, S_p) is connected.

Claim: \mathcal G (\Lambda, S_p) is a tree.

Suppose not, let (v_0, v_1, \cdots, v_k=v_0) a non-trivial cycle. k \geq 2. Since \mathcal G is a Cayley graph, we may assume v_0 = e.

Hence v_1 = \gamma_1, \ v_2 = \gamma_1\gamma_2, \cdots, v_k = \gamma_1 \cdots \gamma_k, for some \gamma_1, \cdots, \gamma_k \in S_p.

Since v_{i-1} \neq v_{i+1} for all 1\leq i \leq k-1, the word \gamma_1, \cdots, \gamma_k cannot contain either \alpha_i\bar{\alpha_i} or \beta_i^2, hence cannot be further reduced.

\gamma_1, \cdots, \gamma_k = e in \Lambda means for some m, n we have

\pm p^n \gamma_1, \cdots, \gamma_k = p^m.

Since every word in \Lambda' with norm N(\alpha) = p^k must have a unique factorization \alpha = \pm p^r w_m where w_m is a reduces word of length m in S'_p and 2r+m = k.

Contradiction. Establishes the claim.

Now we reduce the group \mathbb H (\mathbb Z) mod q:

\pi_q: \mathbb H (\mathbb Z) \rightarrow \mathbb H (\mathbb{F}_q)

One can check that \pi_q(\Lambda') = \mathbb H (\mathbb{F}_q)^\times.

Let Z_q = \{ \alpha \in \mathbb H (\mathbb{F}_q)^\times \ | \ \alpha = \bar{\alpha} \}, Z_q < \mathbb H (\mathbb{F}_q)^\times is a central subgroup.

For \alpha, beta \in \Lambda', \alpha \sim \beta \Rightarrow \pi_q(\alpha)^{-1}\pi_q(\beta) \in Z_q. Which means we have well defined homomorphism

\Pi_q: \Lambda \rightarrow \mathbb H (\mathbb{F}_q)^\times / Z_p.

Let T_{p,q} = \Pi_q(S_p), if q > 2\sqrt{q} we have \Pi_q is injective on S_p and hence $latex | T_{p,q} | = p+1.

Now we are ready to define our expanding family:

X^{p,q} = \mathcal{G}( \Pi_q(\Lambda), T_{p,q}).

Since S_p generates \Lambda, T_{p,q} generates \Pi_q(\Lambda). Hence X^{p,q} is (p+1)-regular and connected.

Theorem 1: g(X^{p,q}) \geq 2 \log_p(q)

Let (e, v_1, \cdots, v_k=e) be a cycle in X^{p,q}, there is t_1, \cdots, t_k \in T_{p,q} such that v_i = t_1 t_2 \cdots t_k for 1 \leq i \leq k.

Let \gamma_i = \Pi_q^{-1}(t_i), \ \gamma_i \in S_p, \alpha = a_0 + a_1 i+a_2 j +a_3 k = \gamma_1 \cdots \gamma_k \in \Lambda. Note that from the above arguement we know \alpha is a reduced word, hence \alpha \neq e_{\Lambda}. In particular, this implies a_1, a_2, a_3 cannot all be 0.

Also, since \alpha is reduced, \displaystyle N(\alpha) = \Pi_{i=1}^k N(\gamma_i) = p^k.

By Lemma, since \Pi_q(\alpha) = 1, \alpha \in \mbox{ker}(\Pi_q) hence q divide a_1, a_2, a_3, we conclude

N(\alpha) = a_0^2 + a_1^2 +a_2^2 +a_3^2 \geq q^2

We deduce p^k \geq q^2 hence k \geq \log_p(q) for all cycle. i.e. g(X^{p,q}) \geq \log_p(q).

Theorem 2: If q does not divide p and p is not a square mod q (i.e. (\frac{p}{q}) = -1), then g(X^{p,q}) \geq 4 \log_p(q) - \log_p(4).

For any cycle of length k as above, we have N(\alpha) = p^k \equiv a_0^2 (\mbox{mod} \ q), i.e. (\frac{p^k}{q}) = 1.

Since (\frac{p^k}{q}) = ((\frac{p}{q})^k, we have (-1)^k = 1, \ k is even. Let k = 2l.

Note that p^k \equiv a_0^2 (\mbox{mod} \ q^2), we also have

p^{2l} \equiv a_0^2 (\mbox{mod} \ q^2)

Hence p^l \equiv a_0 (\mbox{mod} \ q^2).

Since a_0^2 \leq p^{2l}, |a_0| \leq p^l.

If 2l < 4 \log_p(q) - \log_p(4) we will have p^l < q^2/2. Then |p^l\pm a_0| \leq 2|p^l| < q^2.

But we know that p^l \equiv a_0 (\mbox{mod} \ q^2), one of p^l\pm a_0 must be divisible by q^2, hence 0.

Conclude p^l = \pm a_0, N(\alpha) = p^k = a_0^2, hence a_1=a_2=a_3=0. Contradiction.

The Carnot-Carathéodory metric

Conan7 Comments

I remember looking at Gromov’s notes “Carnot-Carathéodory spaces seen from within” a long time ago and didn’t get anywhere. Recently I encountered it again through professor Guth. This time, with his effort in explaining, I did get some ideas. This thing is indeed pretty cool~ So I decided to write an elementary introduction about it here. We will construct a such metric in \mathbb{R}^3.

In general, if we have a Riemannian manifold, the Riemannian distance between two given points p, q is defined as

\inf_\Gamma(p,q) \int_0^1||\gamma'(t)||dt

where \Gamma is the collection of all differentiable curves \gamma connecting the two points.

However, if we have a lower dimensional sub-bundle E(M) of the tangent bundle (depending continuously on the base point). We may attempt to define the metric

d(p,q) = \inf_{\Gamma'} \int_0^1||\gamma'(t)||dt

where \Gamma' is the collection of curves connecting p, q with \gamma'(t) \in E(M) for all t. (i.e. we are only allowed to go along directions in the sub-bundle.

Now if we attempt to do this in \mathbb{R}^3, the first thing we may try is let the sub-bundle be the say, xy-plane at all points. It’s easy to realize that now we are ‘stuck’ in the same height: any two points with different z coordinate will have no curve connecting them (hence the distance is infinite). The resulting metric space is real number many discrete copies of \mathbb{R}^2. Of course that’s no longer homeomorphic to \mathbb{R}^3.

Hence for the metric to be finite, we have to require accessibility of the sub-bundle: Any point is connected to any other point by a curve with derivatives in the E(M).

For the metric to be equivalent to our original Riemannian metric (meaning generate the same topology), we need E(M) to be locally accessible: Any point less than \delta away from the original point p can be connected to p by a curve of length < \varepsilon going along E(M).

At the first glance the existence of a (non-trivial) such metric may not seem obvious. Let’s construct one on \mathbb{R}^3 that generates the same topology:

To start, we first identify our \mathbb{R}^3 with the 3 \times 3 real entry Heisenberg group H^3 (all 3 \times 3 upper triangular matrices with “1”s on the diagonal). i.e. we have homeomorphism

h(x,y,z) \mapsto \left( \begin{array}{ccc} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{array} \right)

Let g be a left-invariant metric on H_3.

In the Lie algebra T_e(H_3) (tangent space of the identity element), the elements X = \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) , Y = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array} \right) and Z = \left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) form a basis.

At each point, we take the two dimensional sub-bundle E(H_3) of the tangent bundle generated by infinitesimal left translations by X, Y. Since the metric g is left invariant, we are free to restrict the metric to E(M) i.e. we have ||X_p|| = ||Y_p|| = 1 for each p \in M.

The interesting thing about H_3 is that all points are accessible from the origin via curves everywhere tangent to E(H_3). In other words, any points can be obtained by left translating any other point by multiples of elements X and Y.

The “unit grid” in \mathbb{R}^3 under this sub-Riemannian metric looks something like:

Since we have

\left( \begin{array}{ccc} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & x+1 & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{array} \right) ,

the original x-direction stay the same, i.e. a bunch of horizontal lines connecting the original yz planes orthogonally.

However, if we look at a translation by Y, we have

\left( \begin{array}{ccc} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & x & z+x \\ 0 & 1 & y+1 \\ 0 & 0 & 1 \end{array} \right)

i.e. a unit length Y-vector not only add a 1 to the y-direction but also adds a height x to z, hence the grid of unit Y vectors in the above three yz planes look like:

We can now try to see the rough shape of balls by only allowing ourselves to go along the unit grid formed by X and Y lines constructed above. This corresponds to accessing all matrices with integer entry by words in X and Y.

The first question to ask is perhaps how to go from (0,0,0) to (0,0,1). –since going along the z axis is disabled. Observe that going through the following loop works:

We conclude that d_C((0,0,0), (0,0,1)) \leq 4 in fact up to a constant going along such loop gives the actual distance.

At this point one might feel that going along z axis in the C-C metric is always takes longer than the ordinary distance. Giving it a bit more thought, we will find this is NOT the case: Imagine what happens if we want to go from (0,0,0) to (0,0,10000)?

One way to do this is to go along X for 100 steps, then along Y for 100 steps (at this point each step in Y will raise 100 in z-coordinate, then Y^{-100} X^{-100}. This gives d_C((0,0,0), (0,0,10000)) \leq 400.

To illustrate, let’s first see the loop from (0,0,0) to (0,0,4):

The loop has length 8. (A lot shorter compare to length 4 for going 1 unit in z-direction)

i.e. for large Z, it’s much more efficient to travel in the C-C metric. d_C( (0,0,0), (0,0,N^2)) = 4N

In fact, we can see the ball of radius N is roughly an rectangle with dimension R \times R \times R^2 (meaning bounded from both inside and outside with a constant factor). Hence the volume of balls grow like R^4.

Balls are very “flat” when they are small and very “long” when they are large.