Sumsets, in discrete and continuous settings

Conan4 Comments

In the past few years, there are 137 papers with the term ‘sumset’ in its title; and 50 more with ‘sum-set’. Ok the above statement was stolen from a talk I happen to be sitting in, by Noga Alon.

As usual, in the middle of the talk I got carried away by some ‘trivial facts’ he wrote down which are only slightly related to the main content. So I thought about that for during the rest of the talk (and also a little bit afterwards).

This time the curious point pops up when he was motivating why people should be studying chromatic number of random Cayley graphs by its application to sumsets.

Definition: In a vector space X, a sumset S \subseteq X is a set that can be represented as the Minkowski sum of another set with itself. i.e. S = A+A where A+A = \{ a_1+a_2 \ | \ a_1, a_2 \in A \}.

It was mentioned that given a large p, if we look at sets in \mathbb{Z}_p, then all sets with large cardinality must be sumsets.

This fact is first published by Ben Green who also raised the natural question:

Question: What’s the lower bound M(p) such that all subsets S \subseteq \mathbb{Z}_p with |S| > M(p) must be a sumset?

Let’s first see why all sets of large cardinality must be sumsets: Well as we all know \mathbb{Z}_p = \mathbb{Z}_p + \mathbb{Z}_p (can also be expressed as many other sums) is a sumset. Hence the first non-trivial case is \mathbb{Z}_p \backslash \{x\}:

The way I think of sumsets is that they are projections of product sets in the angle 3/4 \pi:

Hence our goal is to make up a set S_x such that the projection, after mod p, is everything except for the point x. Well, this isn’t too hard, first note the image of the ‘interval’ \{ x+1, x+2, \cdots, p+x-1 \} after mod p is exactly the set we wanted. Now we just need to make A \times A project to the interval! A = \{ x/2 +1, x/2 + 2, \cdots (p+x)/2 -1 \} will do. (Here by C/2 we meant that it’s the integer C/2 when C is even and (C+p)/2 when it’s odd.

Note that since x \in \mathbb{Z}_p, A + A is actually a square in \{ 0, 1, \cdots, p-1 \}^2 and only “warped” in mod p after we project it to \{ 0, 1, \cdots, 2p-2 \}.

So we just showed all sets with one missing element is a sumset~ Now let’s move to sets of size p-2…(Don’t worry, I’m not going on to 3 and the length of this post will be finite :-P)

In contrast to the above argument which actually works in the continuous setting and shows the Lie group S^1 missing any interval is a sumset, this time we actually need to use the fact that our space is discrete and finite.

Note first that the property of being a sumset is invariant under scaling and translating by an integer. Indeed,

n\cdot S = \{ ns \ | \ s \in S \}

= \{n(a_1+a_2) \ | \ a_1, a_2 \in A\} = n \cdot A + n \cdot A

and of course S+t = (A+t/2) + (A+t/2).

Now no matter which two points a,b we delete, i.e. S = \mathbb{Z}_p \backslash \{a, b \}, we may let S' = (b-a)^{-1} \cdot (S-a). We have S' = \mathbb{Z}_p \backslash \{0, 1\}, which is the projection of the square I^2 = \{ 1,2, \cdots, (p-1)/2 \}^2.

Hence S = [(b-a) \cdot I + a/2] + [(b-a) \cdot I + a/2] is a sumset.

After playing around with the torus for a little bit, I believe in the continue case we can still write S^1 deleting two (small) intervals as a sumset A+A where A is a union of no more than 4 intervals. There are quite a few cases involved concerning the spacing between small intervals, hence I’ll just draw an example:

(By the way, this is about as far as I got daydreaming during the lecture, the rest came from the sources I looked up afterwards.)

Unfortunately since the scaling and translating gived only two degrees of freedom, the above argument fails when considering sets missing three points. (Playing with torus as I first tried, however, might still work)

Back to our question, so now we know at least M_p < p-2 the natural thing to study is of course how does it grow with p. Recall that we denoted M_p = p - f(p), hence the problem is equivalent to giving asymptotic lower bounds for f(p).

So this is quite curious, what do you think? Is f(p) just a counstant? (such as 2, or 3?) Or is it always more than a fixed proportion of \mathbb{Z}_p? (say any set containing 99% of the elements must be a sumset?) Or something in-between?

As one might have expected, f(p) is more than a constant,

Theorem: (Green) f(p) \geq \frac{1}{9} \log_2(p).

It’s also not as large as a fixed percentage:

Theorem: (Gowers-Green) f(p) \leq C \cdot p^2/3 \log(p)

So it’s something ‘in-between’. Interesting…So what is this number? This is an open question in general, by applying methods of Cayley graphs and their spectrums, the speaker (of the talk) was able to improve the above bounds (in this other paper):

Theorem: (Alon) c \cdot \sqrt{\frac{p}{\log{p}}} \leq f(p) \leq C \cdot \frac{ p^2/3}{ \log(p)^{1/3}}

However one should expect that

Conjecture: (Green) f(p) \sim p^{1/2+O(1)}.

Having knowing absolutely nothing about the subject (or combinatorics in general), my first reaction about this is that perhaps, if we look at \mathbb{Z}_p where p is roughly N^2, let S be the set missing N equally spaced points, now if we want to write S as a sumset that’s like finding a product A \times A \subseteq \mathbb{T}^2 that misses all N diagonal circles and have at least N points in each thin strip to ‘block’ every diagonal circle in the strip.

I think this set looks (by the same philosophy as when we play around with the two intervals on the tori case) fairly hard to express as a sum. i.e. when we are exactly in \mathbb{Z}_{N^2}, we can probably ‘just’ do it by choosing one representative from each mod N class and place them in the N strips. But looks as if the ‘resolution’ is any lower, (i.e. p is a little smaller and we still have about N equally spaced holes), we would not have enough freedom to place the points.

Anyways, that last remark might be completely nonsense~ The conjecture is interesting, tho.

4 thoughts on “Sumsets, in discrete and continuous settings”

    • Ah…Sorry Peter,

      I’m still making them >.< (a little behind with homework grading) should be up in about a couple days…

      :-P Not just you~ i should thank you for being continuously checking out the blog though!

      Like

      Reply

      • Ah — that explains it! Hope the grading will go quickly.

        My pleasure to read your blog! There aren’t enough graduate students blogging (speaking as part of mathblogging.org) — certainly not enough with your enthusiasm and quality!

        Like

  2. With first glance on this blog we thought it is some thing about the geometric explanation of hardy-litterwood-sobelev inequality or the generated version of lieb. But when I read it carefully I find it is something about a Green’s conjecture. The explanation of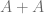 A+A by the projection of A\times A is amazing!

    Like

    Reply

Leave a comment