Tag: link

When k looks and smells like the unknot…

Conan5 Comments

Valentine’s day special issue~ ^_^

Professor Gabai decided to ‘do some classical topology before getting into the fancy stuff’ in his course on Heegaard structures on 3-manifolds. So we covered the ‘loop theorem’ by Papakyriakopoulos last week. I find it pretty cool~ (So I started applying it to everything regardless of whether a much simpler argument exists >.<)

Let M be a three dimensional manifold with (non-empty) boundary. In what follows everything is assumed to be in the smooth category.

Theorem: (Papakyriakopoulos, ’58)
If f: \mathbb{D}^2 \rightarrow M extends continuously to \partial \mathbb{D} and the image f(\partial \mathbb{D}) \subseteq \partial M is homotopically non-trivial in \partial M. Then in any neighborhood N(f(\mathbb{D})) we can find embedded disc D \subseteq M such that \partial D is still homotopically non-trivial in \partial M.

i.e. this means that if we have a loop on \partial M that is non-trivial in \partial M but trivial in M, then in any neighborhood of it we can find a simple loop that’s still non-trivial in \partial M and bounds an embedded disc in M.

We apply this to the following:

Corollary: If a knot k \subseteq \mathbb{S}^3 has \pi_1(\mathbb{S}^3 \backslash k) = \mathbb{Z} then k is the unknot.

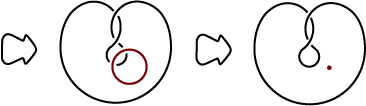
Proof: Take tubular neighborhood N_\varepsilon(k), consider M=\mathbb{S}^3 \backslash \overline{N_\varepsilon(k)}, boundary of M is a torus.

By assumption we have \pi_1(M) = \pi_1(\mathbb{S}^3 \backslash k) = \mathbb{Z}.

Let k' \subseteq \partial M be a loop homotopic to k in N_\varepsilon(k).

Since \pi_1(M) = \mathbb{Z} and any loop in M is homotopic to a loop in \partial M = \mathbb{T}^2. Hence the inclusion map i: \pi_1(\mathbb{T}^2) \rightarrow \pi_1(M) is surjective.

Let l \subseteq \partial M be the little loop winding around k.

It’s easy to see that i(l) generates \pi_1(M). Hence there exists n s.t. k'-n \cdot l = 0 in \pi_1(M). In other words, after n Dehn twists around l, k' is homotopically trivial in M i.e. bounds a disk in M. Denote the resulting curve k''.

Since k'' is simple, there is small neighborhood of k'' s.t. any homotopically non-trivial simple curve in the neighborhood is homotopic to k''. The loop theorem now implies k'' bounds an embedded disc in M.

By taking a union with the embedded collar from k to k'' in N_\varepsilon(k):

We conclude that k bounds an embedded disc in \mathbb{S}^3 \backslash k hence k is the unknot.

Establishes the claim.

Happy Valentine’s Day, Everyone! ^_^

On Whitehead-type manifolds

Conan3 Comments

As I was trying to understand the Whitehead manifold and related constructions of non-tame manifolds batter, I guess it makes a cool blog post ^^

The Whitehead manifold is an example of a 3-manifold that’s contractable but not homeomorphic to \mathbb{R}^3 i.e. the manifold is homotopically equivalent to a point but not tame. (See the earlier post on tameness for more explanations)

Construction:
Take a solid torus T_1 \subseteq \mathbb{R}^3, embed a thinner torus T_2 \subseteq T_1 as shown:

Iterate the process: at each step, embed solid torus T_i into T_{i-1} so that T_i “links with itself” inside T_{i-1}:

Let the Whitehead continuum be the intersection of the T_is.

i.e. \displaystyle W=\bigcap_{i=1}^\infty T_i

As some people know, I have a weird hobby of describing strange continua in terms of Cantor sets…So here comes ‘Conan’s translation’ of the Whitehead continuum:

Take two copies of C \times [0,1] where C is the standard middle-third Cantor set. Bend them into Rainbow-shape with the open ends facing each other:

(I think of this as having a width 1 ‘brush’ with ink only on the points of the Cantor set, and use the brush to draw two semicircles)

Now we connect the open ends: take a width 1/3 brush and connect the top pair of ends so that they link with each other, and then a width 1/9 brush for the highest remaining pair, etc. Take the union of all those connecting sets, union a line segment joining the bottom-most pair of points, we get the Whitehead continuum:

The Whitehead manifold is the complement of W in the three-sphere \mathbb{S}^3, equipped with the

What’s the fundamental group of the Whitehead manifold?

Claim: T_i^c is null-homotopic in T_{i+1}^c.

pf: T_1^c is contractible to a loop in T_{i+1}^c, hence it suffice to homotope the red loop to a point without touching the black loop:

Note that for homotopy, the loop is allowed to pass through itself: (in contrast to isotopy)

The loop can now be easily contracted:

Hence we deduce the Whitehead manifold is null-homotopic. (by collapsing each T_1 at some finite time)

In particular, it has trivial fundamental group! (This might seem hard to believe especially when looking at my Cantor-set picture) Infact for this, we can directly see from the picture that all loop can be homotoped to constant:

Since loop is compact, there is a ‘finest gap’ in the Cantor set which the loop passes through, say it’s a gap with width 1/3^i. Now by performing the operation above, we can homotope all parts of the loop that goes through the 1/3^i to segments that goes through 1/3^{i-1}-gaps, by having the segments crossing themselves once. Now we pass to the 1/3^{i-2}-gaps, etc. until the loop lie completely outside the thickened disc which the continua lies in. Once it’s outside the disc, the loop can be contracted.

The manifold is not homeomorphic to \mathbb{R}^3 as we can easily see that, unlike in \mathbb{R}^3, the red loop in picture cannot be isotoped to a trivial loop.

As an alternative point of view, we should note that in fact T_i^c and T_{i+1} form a thickened Whitehead link:

Since the Whitehead link is symmetric, this gives an simpler (but less direct, in my opinion) way of knowing that red loop is homotopically trivial in the complement of the black loop. (As the black loop is obviously homotopically trivial in the complement of the red loop.)

In light of this, one may construct many different non-tame manifolds with finitely generated fundamental group by embedding a handlebody inside another copy of itself and take the complement of the infinite intersection.

Here is an example of embedding a genus 3 handlebody. The resulting manifold (after taking the complement of the intersection) is a homotopy genus 2 handlebody. (As in the whitehead case, T_i^c can be homotoped to a genus 2 handlebody inside T_{i+1}^c. The ‘third loop’ can be unknotted by crossing itself once.) But it’s of coruse not homeomorphic to the genus 2 handlebody.

A hyperbolic structure on the Whitehead link completement

Conan1 Comment

I’ve been going through Thurston’s book ‘The Geometry and Topology of Three-Manifolds‘ in a reading course with Amie Wilkinson. In Chapter 3, p32, when he’s constructing a hyperbolic structure on the Whitehead link complement, there is a picture on how to glue the 2-cells to the knot, to quite Thurston, ‘the attaching map for the two-cells are indicated by the dotted lines.’ However, for me it’s impossible to see where are the dotted lines going. So I reconstruct it here with some more clear pictures. The construction itself was a cool reading that I wish to share.

First, we have the Whitehead link, looking like the first figure below:

We attach three 1-cells (line segments) as in the second figure, note that the ‘x’ in the middle represents a line segment orthogonal to the screen, connecting the top and bottom line in the figure ‘8’ loop.

Now we will start to attach four 2-cells to the 1-complex above: First, we attach a 2-cell spanning the top part of the figure ‘8’ loop, spanning one side of the middle segment and two sides of the top segment (denote this by cell A):

Do the same with the bottom half (cell B). Note that each cell is attached to three edges, hence they are triangles without vertices in the knot complement with three one-cells attached.

For the other two cells, we attach as follows (cells C and D):

Combining the four 2-cells, we get something like the figure showed below. Note that at the top, cell A is under cell C in the left, intersecting the surface spanned by cells C and D at the edge, and comes above cell D to the right of the edge.

It’s easy to see that the complement of the above 2-complex does not separate \mathbb{R}^3, hence it’s a 3-cell with eight faces (i.e. it has to go through both sides of each 2-cell in order to fill the 3-space) each of its face has three edges. Hence we may glue an octahedron to the 2-complex after the gluing, pairs of faces of the octahedron will be identified groups of four edges will be identified to single edges. Hence to put a hyperbolic structure on the link complement, it suffice to put an hyperbolic structure to the octahedron with vertices deleted.

Since each edge is glued up by four edges of the octahedron, it suffice to find an octahedron (without vertices) in the hyperbolic 3-space that has all adjacent faces intersect in dihedral angle 2 \pi / 4 i.e. all adjecent faces are orthogonal in the hyperbolic space. But this is achieved if we inscribe the regular octahedron into the Klein model (also called projective model of hyperbolic 3-space.

The gluing map for the faces are merely rotations and reflections of the ball which are certainly hyperbolic isometries. Hence this gives a hyperbolic structure to the link complement.