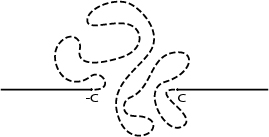Month: November 2010

On length and volume

Conan2 Comments

About a year ago, I came up with an simple argument for the following simple theorem that appeared in a paper of professor Guth’s:

Theorem: If U is an open set in the plane with area 1, then there is a continuous function f from U to the reals, so that each level set of f has length at most 10.

Recently a question of somewhat similar spirit came up in a talk of his:

Question: Let \langle \mathbb{T}^2, g \rangle be a Riemannian metric on the torus with total volume 1, does there always exist a function f: \mathbb{T}^2 \rightarrow \mathbb{R} s.t. each level set of f has length at most 10?

I have some rough thoughts about how might a similar argument on the torus look like, hence I guess it would be a good idea to review and (somewhat carefully) write down the original argument. Since our final goal now is to see how things work on a torus (or other manifolds), here I would only present the less tedious version where U is bounded and all boundary components of U are smooth Jordan curves. Here it goes:

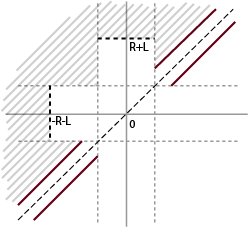
Proof: Note that if a projection of U in any direction has length (one-dimensional measure) \leq 10, then by taking f to be the projection in the orthogonal direction, all level sets are straight with length \leq 10 (see image below).

Hence we can assume any 1-dimensional projection of U has length \geq 10. A typically bad set would ‘span’ a long range in all directions with small area, it can contain ‘holes’ and being not connected:

Project U onto x and y-axis, by translating U, we assume \inf \pi_x(U) = \inf \pi_y(U) = 0. Look at the measure 1 set S in the middle of \pi_y(U) (i.e. a measure 1 set [a,b] \cap \pi_y(U) with the property m_1(\pi_y(U) \cap [0,a]) = m_1(\pi_y(U) \cap [b, \infty])

By Fubini, since the volume \pi_y^{-1}(S) is at most 1, there must be a point p\in S with m_1(\pi_y^{-1}(p))\leq 1:

Since the boundary of U is smooth, we may find a very small neighborhood B_\delta(p) \subseteq \mathbb{R} where for each q \in B_\delta(p), m_1(\pi_y^{-1}(q) \leq 1+\epsilon. (we will call this pink region a ‘neck’ of the set for it has small width and is roughly in the middle)

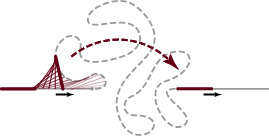
Now we define a \varphi_1: U \rightarrow \mathbb{R}^2 that straches the neck to fit in a long thin tube (note that in general \pi_y(U) may not be connected, but everything is still well-defined and the argument does go through.) and then bend the neck to make the top chunk vertically disjoint from the bottom chunk.

We can take \varphi so that \varphi^{-1} sends the vertical foliation of \varphi(U) to the following foliation in U (note that here we drew the neck wider for easier viewing, in fact the horizontal lines are VERY dense in the neck).

If the y-projection of the top or bottom chunk is larger than 2, we repeat the above process t the chunks. i.e. Finding a neck in the middle measure 1 set in the chunk, starch the neck and shift the top chunk, this process is guaranteed to terminate in at most m_1(\pi_y(U)) steps. The final \varphi sends U to something like:

Where each chunk has y-width L between 1 and 2.

Define f = \pi_x \circ \phi.

Claim: For any c \in \mathbb{R}, m_1(f^{-1}(c)) \leq 5.

The vertical line x=c intersects \varphi(U) in at most one chunk and two necks, taking \varphi^{-1} of the intersection, this is a PL curve C with one vertical segment and two horizontal segment in U:

The total length of f^{-1}(c) = C \cap U is less than 2+2\delta (length of U on the vertical segment) + 2 \times (1+\epsilon) (length of U on each horizontal segment). Pick \epsilon, \delta both less than 1/4, we conclude m_1(f^{-1}(c)) < 5.

Establishes the theorem.

Remark:More generally,any open set of volume V has such function with fibers having length \leq 5 \sqrt{V}. T he argument generalizes by looking at the middle set length \sqrt{V} set of each chunk.

Moving to the torus

Now let’s look at the problem on \langle \mathbb{T}^2, g \rangle, by the uniformization theorem we have a flat torus T^2 = \mathbb{R}^2/\Gamma where \Gamma is a lattice, \mbox{vol}(T^2) = 1 and a function h: T^2 \rightarrow \mathbb{R}^{+} s.t. \langle T^2, h g_0 \rangle is isometric to \langle \mathbb{T}^2, g \rangle. g_0 is the flat metric. Hence we only need to find a map on T^2 with short fibers.

Note that

\int_{T^2} h^2 d V_{g_0} = 1

and the length of the curve \gamma from p to q in \langle T^2, h \dot{g_0} \rangle is

\int_I h |\gamma'(t)| dt.

 

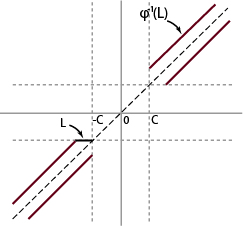
Consider T^2 as the parallelogram given by \Gamma with sides identified. w.l.o.g. assume one side is parallel to the x-axis. Let L be a linear transformation preserving the horizontal foliation and sends the parallelogram to a rectangle.

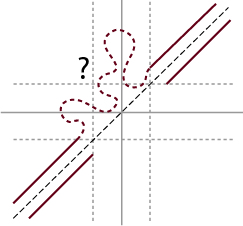
Let F be a piece-wise isometry that “folds” the rectangle:

(note that F is four-to-one except for on the edges and the two medians)
Since all corresponding edges are identified, $lates F$ is continuous not only on the rectangle but on the rectangular torus.

Now we consider F \circ L, pre-image of typical horizontal and vertical lines in the small rectangle are union of two parallel loops:

Note that vertical loops might be very long in the flat T^2 due to the shear while the horizontal is always the width.

(to be continued)

The moving needle problem

ConanLeave a comment

First, let’s clarify that this post has nothing to do with the Kakeya conjecture (except for the word ‘needle’ in it). Anyways, I was asked the following question via an e-mail from Charles this summer: (It turns out that the question was invented by Jonathan King and then communicated to Morris Hirsch and that’s where Charles heard about it from) In any case, I find the problem quite cute:

Problem: Given a smoothly embedded copy of \mathbb{R} in \mathbb{R}^3 containing \{ (x,0,0) \ | \ x \in (-\infty,-C] \cup [C, \infty) \}. Is it always possible to continuously slide a unit length needle lying on the ray (-\infty, -C] to the ray [C, \infty), while keeping the head and tail of the needle on the curve throughout the process?

i.e. the curve is straight once it passes the point (-C, 0) and (C,0), but can be bad between the two points:

We are interested in sliding the needle from the neigative x-axis to the positive x-axis:

Exercise: Try a few examples! It’s quite amusing to see that sometimes both ends of the needle needs to go back and forth along the curve many times, yet it always seem to get through.

One should note that this is not possible if we just require the curve to be eventually straight and goes to infinity at both ends. As we can see on a simple ‘hair clip’ curve:

The curve consists of two parallel rays of distance <1 apart, connected with a semicircle. A unit needle can never get from one ray to the other since the needle would have to rotate 180 degrees and hence it has to be vertical at some point in the process, but no two points on the curve has vertical distance 1.

After some thought, I think I can show for each given curve, 'generic' needle length can pass through:

Claim: For any C^2 embedding as above, there is a full measure and dense G_\delta set \mathcal{L} \subseteq \mathbb{R} of lengths where the needle of any length L \in \mathcal{L} can slide through the curve.

Proof: Let \gamma: \mathbb{R} \rightarrow \mathbb{R}^3 be a smooth parametrization of the curve s.t. \gamma(t) = t for t \in (-\infty, -C] \cup [C, \infty).

Define \varphi: \mathbb{R}^2 \rightarrow \mathbb{R} where \varphi: (s, t) \mapsto d(\gamma(s), \gamma(t)).

Hence \varphi vanishes on the diagonal and takes positive value everywhere else.
Since \gamma(t) = t for t \notin (-C, C), hence \varphi(s,t)=|s-t| for |s|, |t|>C. \varphi^{-1}(L) contains four rays \{ |s-t| = L \ | \ s, t \notin (-C, C) \}:

Observation: a needle of length L can slide through the curve iff there is a continuous path in the level set \varphi(p) = L connecting the two rays above the diagonal. (This is merely projection onto the x and $larex y$-axis.)

We also have \varphi is C^2 other than on the diagonal. (It behaves like the absolute value function near the diagonal). By Sard’s theorem, since \varphi is C^2 on \{s < t\}, the set of critical values is both measure 0 and first category.

Let \mathcal{L} be the set of regular values of \varphi. For any L \in \mathcal{L}, by implicit function theorem, the level set \varphi^{-1}(L) is a C^2 sub-manifold.

Since the arc \gamma([-C, C]) is compact, we can find large R where \gamma([-C, C]) \subseteq B(\bar{0}, R).

Hence for |t| > R + L and s \in [-C, C], we have

\varphi (s, t) = d(\gamma(s), \gamma(t)) > d(\gamma(t), B(\bar{0}, R)) > L

The same holds with |s| > R + L and t \in [-C, C]

i.e. \varphi takes value >L in the shaded region below:

Hence for L \in \mathcal{L}, \varphi^{-1}(L) \cap \{x \leq y\} is a 1 dimensional sub-manifold, outside a bounded region it contains only two rays. We also know that the level set is bounded away from the diagonal since \varphi vanishes on the diagonal. By an non-ending arc argument, one connected component of \varphi^{-1}(L) must be a curve connecting the end points of the two rays. Establishes the claim.

Remarks: This problem happens to come up at the very end (questio/answer part) of Charles’s talk in the midwest dynamics conference last month (where he talked about our joint work about funnel sections). A couple weeks later Michal Misiurewicz e-mailed us a counter-example when the curve is not smooth (only continuous).

Initially I tried to use the above argument to get the length 1 needle. Everything works fine until a point where one has a continuum in the level set connecting the end-points of the two rays. We want the continuum to be path connected. I got stuck on that. In the continuous curve case, Michal’s counter-example corresponds to the continuum containing a \sin(1/x) curve, hence is not path connected.

I believe such thing cannot happen for smooth. The hope would be that the length 1 needle can slide through any C^2 (or C^1) curve. (Note that once the length 1 needle can pass through, then all length can pass through just by rescaling the curve.) In any case, still trying…

Coding Fractals by trees

ConanLeave a comment

Recently I’ve been editing a set of notes taken by professor Kra during Furstenberg’s course last year. (Well…I should have done this last year >.<) One of the main ideas in the course was to build a correspondence between trees and Fractal sets – and hence enables one to prove statements about dimensions and projections of Fractals by looking at the corresponding trees. I want to sketch some highlights of the basic idea here.

Let Q=Q^{(n)} denote the unit cube in \mathbb{R}^{n}.

Let A\subset\mathbb{R}^{n} and x\in A. For t\in\mathbb{R}, consider the family
t(A-x)\cap Q.

Question:Does the limit exist as t\to\infty? (here we consider the Hausdorff limit on compact subsets of Q)

i.e. we ‘zoom in’ the set around the point x, always crop the set to the cube Q and consider what does the set ‘look like’ when the strength of the magnifying glass approaches infinity.

Example:
If A is smooth (curve of surface), then this limit exists and is a subspace intersected with Q.

Generally one should not expect the above limit to exist for fractal sets, however if we weaken the question and ask for the limit when we take a sequence (n_k)\rightarrow\infty, then it’s not hard to see self-similar sets would have non-trivial limits. Hence in some sense fractal behavior is characterized by having non-trivial limit sets.

Definition: Let A\subset Q^{(n)},
A' is a mini-set of A if for some \lambda\geq 1 and u\in\mathbb{R}^{n}, A' =(\lambda A+u)\cap Q

A'' is a micro-set of A if there is sequence of minisets A'_{n} of A and A'' = \lim_{n\to\infty}A'_{n}

A is homogeneous if all of its microsets are minisets. As we should see below, homogeneous fractals are ‘well-behaved’ in terms of dimensions.

Here comes a version of our familiar definition:

Definition:A set A\subset X has Hausdorff \alpha-measure 0 if for every \varepsilon > 0, there exists a covering of A\subset \bigcup_{n=1}^{\infty}B_{\rho_{n}} with \sum_{n}\rho_{n}^{\alpha} \alpha.

Thus it makes sense to define:

Definition: The Hausdorff dimension of A is

\dim(A) = \inf\{\alpha>0\colon \text{Hausdorff } \alpha \text{ measure is } 0 \}.

Now comes trees~ For A\subset[0,1] closed, consider expansion in base 3 of numbers in A. In the expansion of each number in A, there will be certain digits which appear. Following this digit, there may be certain digits that can appear. This defines a tree, which is a tree of shrinking triadic intervals that intersects the set A.

Definition: Let \Lambda be a finite set of symbols (which we will refer to as the alphabet and elements of \Lambda are letters of the alphabet).

A word w is any concatenation of finitely many symbols in \Lambda, the number of symbols in w is called the length of w, denoted by \ell(w).

A tree \tau in the alphabet \Lambda is a set of words satisfying
1. If uv\in\tau then u\in\tau.
2. If u\in\tau, then there exists a letter a\in\Lambda such that ua\in\tau.

Notation: if w\in\tau, denote \tau^{w} = \{v\colon wv\in\tau\}.

Definition: A section \Sigma of \tau is a finite set of words for which there exists N such that if s\in\tau and \ell(s) \geq N, then there exists r\in\Sigma and a word w such that s = rw.

Definition: The Hausdorff dimension of a tree is defined by \dim(\tau)=\inf\{ \beta \ | \ \inf_{\Sigma}\{\sum_{r\in\Sigma} e^{-\beta\ell(r)}\} = 0 \} where \Sigma is any section of \tau.

Theorem: The Hausdorff dimension of a tree equals the Hausdorff dimension of set it corresponds to.

The proof is merely going through the definition, hence we won’t present here. It suffice to check the dimension is unchanged if we only consider open ball covers with balls of radius $p^{-n}$ for any given $p \in \N$. Which is indeed true.

Now let’s give a simple example to illustrate how to make use of this correspondence:

It is easy to prove \dim(X \times Y) \geq \dim(X) \times \dim(Y), here we produce an example were the inequality is strict.

Let A \subseteq [0,1] be the set of numbers whose decimal expansion vanishes from the k_{2n} to k_{2n+1}-th digits to the right of 0.

To compute \dim(A), look at levels such that a small number of intervals will cover the set A. The number of intervals of size 10^{k_{2n+1}} is less than 10^{k_{2n}}. Then if \frac{10^{k_{2n}}}{k_{2n+1}} goes to 0, we’ll have that the Hausdorff dimension is 0. So we just
need k_{2n}/k_{2n+1}\to 0.

Let B be the set of numbers whose decimals vanish from k_{2n-1} to k_{2n}-1-th digits. By the same computation, \dim(B) = 0.

What about A\times B? The tree that corresponds to this is a regular tree which every point has 10 branches. So the Hausdorff dimension is 1.

Note: Here the structure of the tree gives you easy information on the set, but it is hard to look directly at the set and see this information.

Many theorems regarding dimension of projections and intersections of fractal sets turns out to be simple to prove after we coded the sets by trees.

On Whitehead-type manifolds

Conan3 Comments

As I was trying to understand the Whitehead manifold and related constructions of non-tame manifolds batter, I guess it makes a cool blog post ^^

The Whitehead manifold is an example of a 3-manifold that’s contractable but not homeomorphic to \mathbb{R}^3 i.e. the manifold is homotopically equivalent to a point but not tame. (See the earlier post on tameness for more explanations)

Construction:
Take a solid torus T_1 \subseteq \mathbb{R}^3, embed a thinner torus T_2 \subseteq T_1 as shown:

Iterate the process: at each step, embed solid torus T_i into T_{i-1} so that T_i “links with itself” inside T_{i-1}:

Let the Whitehead continuum be the intersection of the T_is.

i.e. \displaystyle W=\bigcap_{i=1}^\infty T_i

As some people know, I have a weird hobby of describing strange continua in terms of Cantor sets…So here comes ‘Conan’s translation’ of the Whitehead continuum:

Take two copies of C \times [0,1] where C is the standard middle-third Cantor set. Bend them into Rainbow-shape with the open ends facing each other:

(I think of this as having a width 1 ‘brush’ with ink only on the points of the Cantor set, and use the brush to draw two semicircles)

Now we connect the open ends: take a width 1/3 brush and connect the top pair of ends so that they link with each other, and then a width 1/9 brush for the highest remaining pair, etc. Take the union of all those connecting sets, union a line segment joining the bottom-most pair of points, we get the Whitehead continuum:

The Whitehead manifold is the complement of W in the three-sphere \mathbb{S}^3, equipped with the

What’s the fundamental group of the Whitehead manifold?

Claim: T_i^c is null-homotopic in T_{i+1}^c.

pf: T_1^c is contractible to a loop in T_{i+1}^c, hence it suffice to homotope the red loop to a point without touching the black loop:

Note that for homotopy, the loop is allowed to pass through itself: (in contrast to isotopy)

The loop can now be easily contracted:

Hence we deduce the Whitehead manifold is null-homotopic. (by collapsing each T_1 at some finite time)

In particular, it has trivial fundamental group! (This might seem hard to believe especially when looking at my Cantor-set picture) Infact for this, we can directly see from the picture that all loop can be homotoped to constant:

Since loop is compact, there is a ‘finest gap’ in the Cantor set which the loop passes through, say it’s a gap with width 1/3^i. Now by performing the operation above, we can homotope all parts of the loop that goes through the 1/3^i to segments that goes through 1/3^{i-1}-gaps, by having the segments crossing themselves once. Now we pass to the 1/3^{i-2}-gaps, etc. until the loop lie completely outside the thickened disc which the continua lies in. Once it’s outside the disc, the loop can be contracted.

The manifold is not homeomorphic to \mathbb{R}^3 as we can easily see that, unlike in \mathbb{R}^3, the red loop in picture cannot be isotoped to a trivial loop.

As an alternative point of view, we should note that in fact T_i^c and T_{i+1} form a thickened Whitehead link:

Since the Whitehead link is symmetric, this gives an simpler (but less direct, in my opinion) way of knowing that red loop is homotopically trivial in the complement of the black loop. (As the black loop is obviously homotopically trivial in the complement of the red loop.)

In light of this, one may construct many different non-tame manifolds with finitely generated fundamental group by embedding a handlebody inside another copy of itself and take the complement of the infinite intersection.

Here is an example of embedding a genus 3 handlebody. The resulting manifold (after taking the complement of the intersection) is a homotopy genus 2 handlebody. (As in the whitehead case, T_i^c can be homotoped to a genus 2 handlebody inside T_{i+1}^c. The ‘third loop’ can be unknotted by crossing itself once.) But it’s of coruse not homeomorphic to the genus 2 handlebody.

Remarks from the Oxtoby Centennial Conference

Conan1 Comment

A few weeks ago, I received this mysterious e-mail invitation to the ‘Oxtoby Centennial Conference’ in Philadelphia. I had no idea about how did they find me since I don’t seem to know any of the organizers, as someone who loves conference-going, of course I went. (Later I figured out it was due to Mike Hockman, thanks Mike~ ^^ ) The conference was fun! Here I want to sketch a few cool items I picked up in the past two days:

Definition:A Borel measure \mu on [0,1]^n is said to be an Oxtoby-Ulam measure (OU for shorthand) if it satisfies the following conditions:
i) \mu([0,1]^n) = 1
ii) \mu is positive on open sets
iii) \mu is non-atomic
iv) \mu(\partial [0,1]^n) = 0

Oxtoby-Ulam theorem:
Any Oxtoby-Ulam measure is the pull-back of the Lebesgue measure by some homeomorphism \phi: [0,1]^n \rightarrow [0,1]^n.

i.e. For any Borel set A \subseteq [0,1]^n, we have \mu(A) = \lambda(\phi(A)).

It’s surprising that I didn’t know this theorem before, one should note that the three conditions are clearly necessary: A homeo has to send open sets to open sets, points to points and boundary to boundary; we know that Lebesgue measure is positive on open sets, 0 at points and 0 on the boundary of the square, hence any pull-back of it must also has those properties.

Since I came across this at such a late time, my first reaction was: this is like Moser’s theorem in the continuous case! But much cooler! Because measures are a lot worse than differential forms: many weird stuff could happen in the continuous setting but not in the smooth setting.

For example, we can choose a countable dense set of smooth Jordan curves in the cube and assign each curve a positive measure (we are free to choose those values as long as they sum to 1. Now we can define a measure supported on the union of curves and satisfies the three conditions. (the measure restricted to each curve is just a multiple of the length) Apply the theorem, we get a homeomorphism that sends each Jordan curve to a Jordan curve with positive n dimensional measure and the n dimensional measure of each curve is equal to our assigned value! (Back in undergrad days, it took me a whole weekend to come up with one positive measured Jordan curve, and this way you get a dense set of them, occupying a full measure set in the cube, for free! Oh, well…>.<)

Question: (posed by Albert Fathi, 1970)
Does the homeomorphism \phi sending \mu to Lebesgue measure depend continuously on \mu?

My first thought was to use smooth volume forms to approximate the measure, for smooth volume forms, Moser’s theorem gives diffeomosphisms depending continuously w.r.t. the form (I think this is true just due to the nature of the construction of the Moser diffeos) the question is how large is the closure of smooth forms in the space of OU-measures. So I raised a little discussion immediately after the talk, as pointed out by Tim Austin, under the weak topology on measures, this should be the whole space, with some extra points where the diffeos converge to something that’s not a homeo. Hence perhaps one can get the homeo depending weakly continuously on \mu.

Lifted surface flows:

Nelson Markley gave a talk about studying flows on surfaces by lifting them to the universal cover. i.e. Let \phi_t be a flow on some orientable surface S, put the standard constant curveture metric on S and lift the flow to \bar{\phi}_t on the universal cover of S.

There is an early result:

Theorem: (Weil) Let \phi_t be a flow on \mathbb{T}^2, \bar{\phi}_t acts on the universal cover \mathbb{R}^2, then for any p \in \mathbb{R}^2, if \displaystyle \lim_{t\rightarrow \infty} ||\bar{\phi}_t(p)|| = \infty then \lim_{t\rightarrow \infty} \frac{\bar{\phi}_t(p)}{||\bar{\phi}_t(p)||} exists.

i.e. for lifted flows, if an orbit escapes to infinity, then it must escape along some direction. (No sprial-ish or wild oscillating behavior) This is due to the nature that the flow is the same on each unit square.

We can find its analogue for surfaces with genus larger than one:

Theorem: Let \phi_t be a flow on S with g \geq 2, \bar{\phi}_t: \mathbb{D} \rightarrow \mathbb{D}, then for any p \in \mathbb{D}, if \displaystyle \lim_{t\rightarrow \infty} ||\bar{\phi}_t(p)|| = \infty then \lim_{t\rightarrow \infty} \bar{\phi}_t(p) is a point on the boundary of \mathbb{D}.

Using those facts, they were able to prove results about the structure of \omega limiting set of such orbits (those that escapes to infinity in the universal cover) using the geometric structure of the cover.

I was curious about what kind of orbits (or just non-self intersecting curves) would ‘escape’, so here’s some very simple observations: On the torus, this essentially means that the curve does not wind around back and forth infinitely often with compatible magnitudes, along both generators. i.e. the curve ‘eventually’ winds mainly in one direction along each generating circle. Very loosely speaking, if a somewhat similar thing is true for higher genus surfaces, i.e. the curve eventually winds around generators in one direction (and non-self intersecting), then it would not be able to have very complicated \omega limiting set.

Measures on Cantor sets

In contrast to the Oxtoby-Ulam theorem, one could ask: Given two measures on the standard middle-third Cantor set, can we always find a self homeomorphism of the Cantor set, pushing one measure to the other?

Given there are so many homeomorphisms on the Cantor set, this sounds easy. But in fact it’s false! –There are countably many clopen subsets of the Cantor set (Note that all clopen subsets are FINITE union of triadic copies of Cantor sets, a countable union would necessarily have a limit point that’s not in the union), a homeo needs to send clopen sets to clopen sets, hence for there to exist a homeo the countably many values the measures take on clopen sets must agree.

So a class of ‘good measures’ on Cantor sets was defined in the talk and proved to be realizable by a pull back the standard Hausdorff measure via a homeo.

I was randomly thinking about this: Given a non-atomic measure \mu on the Cantor set, when can it be realized as the restriction of the Lebesgue measure to an embedding of the Cantor set? After a little bit of thinking, this can always be done. (One can simple start with an interval, break it into two pieces according to the measure \mu of the clopen sets before and after the largest gap, then slightly translate the two pieces so that there is a gap between them; iterate the process)

In any case, it’s been a fun weekend! ^^