Hi all, life has taken some dramatic turns since I last posted: I did not get to teach topology in Art Center, so I took a different approach in job-finding and ended up making pastries in a local bakery overnight (11pm-7am) for two months until some (very complicated) personal affairs arise, due to an irreversible influence from certain individual, I decided that I should forget about applied/digital art and just paint classically instead; So I think I’ll start by become a painter who also works in random jobs (such as dishwashing). Oh, and I’m getting married sometime this year~
Ok, enough random things about me…I’m here to give a little teaser of a posthumous paper of mine in mathematics before it goes on the ArXiv, which I finally received a complete draft from my wonderful co-authors Alex Lubotzky and Joseph Maher. I hope this summary from my point of view could serve as my tribute to this interesting piece of work.
***********************************************
Let’s start with an ‘unrelated’ piece of history: Once upon a time, many standard or number-theoretically significant graphs (such as Ramanujan graphs, as I might have mentioned when talking about expanders before) were not known to exist, then there comes Paul Erdos, after whom they were known to exist and is literally ‘everywhere’, but we still didn’t manage to ‘catch’ any particular one of them, at least not for another twenty something years. So we know that in mathematics it’s sometimes easier to prove ‘most’ objects satisfy some properties than to pick one out, for establishing existence.
While in Israel, Alex presented to me this fascinating idea he had about proving existential results in topology using random methods:
(crush-course for those who don’t know topology)
1. All closed 3-manifolds can be written as two many-holed solid donuts glued together along their surface.
WHY?
It’s easy to believe all smooth manifolds can be chopped into tiny tetrahedrons.
Take the triangulation -> take it’s 1-skeleton -> take a small neighborhood of the 1-skeleton This is a neighborhood of a graph, hence a handlebody. Now what’s the complement of that 1-skeleton neighborhood?
…also a neighborhood of a graph~! …hence another handlebody…(note that the two donuts must have same number of holes since the gluing is clearly a homeomorphism)
This is called a Heegaard splitting of the 3-manifold.
OK, we now know all 3-manifolds arise from such gluings when we use some (probably large) genus donuts. We can fix a genus and ask what are all possible gluings occurring in that genus.
Now two homotopic homeomorphisms clearly give the same 3-manifold, hence we only need to consider the homotopy classes of surface homeomorphisms, which forms the infamous mapping class group of the surface.
To summarize, we have in hand a discrete group in hand whose elements parametrize (with repetitions) all 3-manifolds given by gluing donuts of that genus.
What can we do on infinite discrete groups? Well, actually many things, but in particular we may put a probability measure on its generators and random walk!
Now we can ask all sorts of things regarding what happens after walking for a long time, such as:
After taking N steps,
How likely are we landing on a gluing map that gives a hyperbolic 3-manifold? (property 1)
How likely is the resulting gluing a Heegaard splitting with minimal genus? (property 2)
Topologists might have the intuition that ‘most’ 3-manifold should be hyperbolic and guess that ‘most’ Heegaard splittings are minimal genus; if so, I’m glad to tell you that…your intuition is correct!
At this point I would like to sidetrack a little bit and point out that, many of those traditional combinatorics/number theory/graph theory random method arguments goes like this: take a smartly chosen class of objects, put a carefully constructed probability distribution on it, and Boom~ ‘most’ (asymptotic probability one) many objects are our desired objects! so they exist!
Now of course we already know that hyperbolic 3-manifolds exist in every Heegaard genus…but we figured that this random implying existence method can be pushed much further than merely most imply exist. After all, it is a group which we are walking on~
First of all, property 1 and 2 are not only generic in the sense of having asymptotic probability 1, but actually the set that does not satisfy property 1 and 2 decreases exponentially, i.e. the exceptional set for both properties have size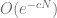 
for some 
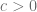after $N$ steps.
The above leads one to think of the possibility of estimating decay rates of various 3-manifold properties under this random walk and thus drew conclusions such as “if property A decays exponentially, property B decays polynomially but not faster, then even if ‘most’ objects satisfy neither A now B, we can still conclude that there exist objects that’s B but not A.
Now this is all very nice but useless unless we can find and prove some manifold properties with interesting, non-exponential decay rates. For that we may take advantage of the group structure: homomorphisms between groups project random walks, hence invariants that take value in a (hopefully simpler) group would have level sets in the mapping class group having decay rates given by return probabilities of the projected Markov processes on the simpler group, which can be polynomial.
In that spirit, we apply our random method to find hyperbolic genus g homology 3-spheres with particular Casson invariants. (I will not get into Casson invariants here, let’s just keep in mind that it’s a classical integer invariant of homology 3-spheres, it is generally pretty hard to construct non-trivial examples with particular Casson invariants) Namely we prove:
Theorem: For any integers 
with 
, there exists hyperbolic homology 3-spheres with Heegaard genus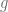 
and Casson invariant 
.
The subgroup of the mapping class group consisting of all elements that give raise to homology 3-spheres is called the Torelli group. So Casson invariant assigns integers to Torelli group elements. With some work one can show that this is somewhat close to a homomorphism to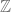 
. More precisely, it’s a homomorphism on what’s called the Johnson kernel, which is a normal subgroup of the Torelli.
Unfortunately little is known about the Johnson kernel, in particular we don’t know if it’s finitely generated. But for our purpose we can pick out three elements from the group and consider the subgroup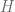 
generated by them. (two Pseudo Anosov elements with distinct stable and unstable laminations, plus a third element that guarantees Casson homomorphism is surjective.)
Now the two Pseudo Anosov elements makes the argument of exponential decay carry through (i.e. property 1 and 2 still holds outside of an exponentially small set in 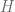); The Casson invariant is a homomorphism hence projects the random walk in 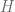to a Markov process on 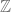. Asymptotically such process hits returns to 
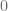with probability 
; making all integers achieved with a quadratic asymptotic decay rate. i.e. all level sets of the Casson homomorphism has decays only quadratically in .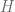
From the above we can conclude there are manifolds with any Casson invariant which falls outside both the exception set of hyperbolic and Heegaard genus .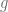
Some slightly more recent results =P:
Area777 